• 8. Апроксимування функцій
  • 8.1. Постановка задачі апроксимації
  • 8.2. Найкраще рівномірне наближення
  • 8.3. Приклади побудови БНРН
  • 8.4. Найкраще середньоквадратичне наближення
  • 8.5. Системи ортогональних функцій
  • 8.6. Середньоквадратичне наближення періодичних функцій
  • 8.7. Метод найменших квадратів (МНК)
  • 8.8. Згладжуючі сплайни

8. Апроксимування функцій

8.1. Постановка задачі апроксимації

Література:

• Бахвалов, Жидков, Кобельков, стор. 164–166: pdf

Наближення функцій застосовують у випадках, якщо

• функція складна (трансцендентна або є розв’язком складної задачі) і її замінюють функцією, яка легко обчислюється (найчастіше, поліномом);

• необхідно побудувати функцію неперервного аргументу для функції, яка задана своїми значеннями (таблична);

• таблична функція наближається табличною ж функцією (згладжування).

Інтерполювання не кращий спосіб наближення функцій через розбіжність цього процесу для поліномів. Тим більше доцільність застосування інтерполювання сумнівна, якщо функція таблична, а її значення неточні. Потрібно будувати апроксимуючу функцію з інших міркувань.

Найбільш загальний принцип: наблизити $f(x)$ функцією $\Phi(x)$ так, щоб досягалася деяка задана точність $\varepsilon$:

\begin{equation} \left| f(x) - \Phi(x) \right| < \varepsilon \end{equation}

Але розв’язок в такій постановці може не існувати або бути не єдиним.

Загальна постановка задачі наближення така. Нехай маємо елемент $f$ лінійного нормованого простору $R$. Побудуємо підпростір $M_n$, в якому елементи є лінійною комбінацією:

\begin{equation} \label{eq:8.1.1} \Phi = \Sum_{i = 0}^n c_i \varphi_i \in M_n \subset R \end{equation}

по елементах лінійно незалежної системи

$$\begin{equation} \left\{ \varphi_i \right\}\void_{i = 0}^\infty, \quad \varphi_i \in R \label{eq:8.1.2}. \end{equation}$$

Відхилення $\Phi \in M_n$ від $f \in R$ є число

\begin{equation} \Delta(f, \Phi) = | f - \Phi |. \end{equation}

Позначимо

\begin{equation} \Inf_{\Phi \in M_n} |f - \Phi| = \Delta (f). \end{equation}

Означення. Елемент $\Phi_0$ такий, що

\begin{equation} \Delta(d, \Phi_0) = |f - \Phi_0| = \Inf_{\Phi \in M_n} |f - \Phi| = \Delta(f), \end{equation}

називається елементом найкращого наближення (ЕНН).

Ясно, що умову точності треба перевіряти на цьому елементі. У випадку її невиконання треба збільшувати кількість елементів $n$ в \eqref{eq:8.1.1}.

Теорема 1: Для будь-якого лінійного нормованого простору $R$ існує елемент найкращого наближення $\Phi_0 \in M_n$.

Доведення: Введемо

\begin{equation} F \left( \vec c \right) = F(c_0, c_1, \ldots, c_n) = |f - \Phi| = \left| f - \Sum_{i = 0}^n c_i \varphi_i \right|. \end{equation}

Це неперервна функція аргументів $\vec c = (c_0, c_1, \ldots, c_n)$. Для елементів, які задовольняють умові

\begin{equation} \label{eq:8.1.4} |\Phi| > 2 |f|, \quad f \in R_1, \quad \Phi \in M_n, \end{equation}

маємо

\begin{equation} F \left( \vec c \right) = |f - \Phi| \ge |\Phi| - |f| > 2 |f| - |f| = |f| > \Delta(f). \end{equation}

Значить ЕНН $\Phi_0 \in \{\Phi: \|\Phi\| \le 2 \|f\|\} = \overline{U} \subset M_n$. За теоремою Кантора $\exists \Phi_0$, де $F \left( \vec c \right)$ досягає мінімуму. Причому $\|f - \Phi_0\| \le \|f - \Phi\|$. $\square$

Елементів найкращого наближення в лінійному нормованому просторі може бути і декілька.

Означення: Простір $R$ називається строго нормованим, якщо з умови

\begin{equation} |f + g| = |f| + |g|, \quad |f| \ne 0, \quad |g| \ne 0 \end{equation}

випливає, що $\exists \lambda \ne 0$ таке, що

\begin{equation} g = \lambda f. \end{equation}

Теорема 2: Якщо простір $R$ строго нормований, то елемент найкращого наближення $\Phi_0$ єдиний.

Доведення: від супротивного. Нехай існують $\Phi_0^{(1)} \ne \Phi_0^{(2)}$ — два елементи найкращого наближення. Візьмемо $\alpha \in [0, 1]$, тоді

$$\begin{equation} \begin{aligned} \Delta(f) & \le \left\| f - \alpha \Phi_0^{(1)} - (1 - \alpha) \Phi_0^{(2)} \right\| = \newline & = \left\| \alpha \left( f - \Phi_0^{(1)} \right) + (1 - \alpha) \left( f - \Phi_0^{(2)} \right) \right\| \le \newline & \le \alpha \left\| f - \Phi_0^{(1)} \right\| + (1 - \alpha) \left\| f - \Phi_0^{(2)} \right\| = \newline &= \alpha \Delta (f) + (1 - \alpha) \Delta (f) = \Delta(f). \end{aligned} \end{equation}$$

Тобто всі «$\le$» можна замінити на «$=$» Отримаємо

\begin{equation} \begin{aligned} & \left| \alpha \left( f - \Phi_0^{(1)} \right) + (1 - \alpha) \left( f - \Phi_0^{(2)} \right) \right| = \newline & \quad \alpha \left| f - \Phi_0^{(1)} \right| + (1 - \alpha) \left| f - \Phi_0^{(2)} \right|. \end{aligned} \end{equation}

За припущенням $\exists \lambda$ таке, що

\begin{equation} \alpha \left( f - \Phi_0^{(1)} \right) + \lambda (1 - \alpha) \left( f - \Phi_0^{(2)} \right). \end{equation}

Виберемо $\alpha = 1 / 2$. Тоді

\begin{equation} f - \Phi_0^{(1)} = \lambda \left( f - \Phi_0^{(2)} \right). \end{equation}

Оскільки

\begin{equation} \left| f - \Phi_0^{(1)} \right| = \left| f - \Phi_0^{(2)} \right| = \Delta(f), \end{equation}

то остання рівність має місце тільки для $\lambda = 1$. Звідси

\begin{equation} f - \Phi_0^{(1)} = f - \Phi_0^{(2)} \implies \Phi_0^{(1)} = \Phi_0^{(2)}. \end{equation}

Отже, ми отримали протиріччя з припущенням, що і доводить існування єдиного елемента найкращого наближення. $\square$

Теорема 3: Гільбертів простір $H$ — строго нормований.

Доведення: Нехай

\begin{align} | f + g | &= |f| + |g|, \label{eq:8.1.6} \newline | f + g |^2 &= |f|^2 + 2 |f| \cdot |g| + |g|^2. \end{align}

З іншого боку

\begin{equation} | f + g |^2 = \langle f + g, f + g\rangle = |f|^2 + 2 \langle f, g \rangle + |g|^2. \end{equation}

Звідси $\|f\| \cdot \|g\| = \langle f, g \rangle$. Для довільного гільбертового простору $\langle f, g\rangle \le \|f\| \cdot \|g\|$.

Таким чином на елементах \eqref{eq:8.1.6} нерівність Коші-Буняковського перетворюється в рівність. Розглянемо

\begin{equation} \begin{aligned} |f - \lambda g|^2 & = |f| - 2 \lambda \langle f, g \rangle + \lambda^2 |g|^2 = \newline & = |f|^2 - \lambda |f| \cdot |g| + \lambda^2 |g|^2 = \newline &= \left( |f| - \lambda |g| \right)^2. \end{aligned} \end{equation}

Тоді для $\lambda = \|f\| / \|g\|$ маємо $\|f - λ g\| = 0$. Звідси $\exists λ$: $f = \lambda g$, тобто $Н$ — строго нормований. $\square$

Наслідок: $R = H \implies \exists! \Phi_0 \in M_n$.

Приклади (строго нормованих просторів):

1. $L_2([a, b])$ з нормою $\|u\| = \sqrt{\Int_a^b u^2 \diff x}$.

2. $L_p([a, b])$ з нормою $\|u\| = \left( \Int_a^b u^p \diff x \right)^{1 / p}$, $p > 1$.

Простір $C([a,b])$ не є строго нормованим, але в ньому існує єдиний елемент найкращого наближення (про цей факт в наступному пункті).

8.2. Найкраще рівномірне наближення

Література:

• Бахвалов, Жидков, Кобельков, стор. 178–187: pdf

Означення: Найкраще рівномірне наближення — це наближення в просторі $R = C([a,b])$, де $\|f\|_{C([a,b])} = \Max_{x \in [a, b]} \vert f \vert$ — рівномірна метрика.

Теорема 1 (Хаара): Для того, щоб $\forall f \in C([a,b])$ існував єдиний елемент найкращого рівномірного наближення необхідно і достатньо, щоб система $\{\varphi_i\}_{i = 0}^\infty$ була системою Чебишова.

Означення: Система $\{\varphi\}_{i = 1}^\infty$ називається системою Чебишова, якщо елемент $\Phi_n(x) = \Sum_{i = 0}^n c_i \varphi_i(x)$ має не більше $n$ нулів, причому $\Sum_{i = 1}^n c_i^2 \ne 0$.

Наприклад, системою Чебишова є поліноміальна система $\{x^i\}\void_{i = 0}^\infty$.

Означення: Позначимо $Q_n^0(x)$ — багаточлен найкращого рівномірного наближення (далі — БНРН.).

Його відхилення від $f$:

$$\begin{equation} \Delta(f) = \left\| Q_n^0 (x) - f(x) \right\|_C = \Inf_{Q_n(x)} \left\| Q_n(x) - f(x) \right\|. \end{equation}$$

Теорема 2 (Чебишова): $Q_n^0(x)$ — БНРН неперервної функції $f(x)$ тоді та тільки тоді, якщо на відрізку $[a,b]$ існує хоча б $(n + 2)$-а точки $a \le x_0 \le \ldots \le x_m \le b$, $m \ge n + 1$ такі, що

\begin{equation} \label{eq:8.2.1} f(x_i) - Q_n^0(x_i) = \alpha (-1)^i \Delta(f), \end{equation}

де $i = \overline{0,m}$, $\alpha = \pm 1$.

Означення: Точки $\{x_i\}_{i=0}^m$, які задовольняють умовам теореми Чебишова, називаються точками чебишовського альтернансу.

Теорема 3: $Q_n^0(x)$ — БНРН для неперервної функції єдиний.

Доведення: Припустимо, існують два БНРН степеня $n$: $Q_n^{(1)}(x) \ne Q_n^{(2)}(x)$:

\begin{equation} \Delta(f) = \left| f - Q_n^{(1)} \right|\void_C = \left| f - Q_n^{(2)} \right|\void_C. \end{equation}

Звідси випливає, що

\begin{equation} \left| f - \frac{Q_n^{(1)}(x) + Q_n^{(2)}(x)}{2} \right| \le \left| \frac{f - Q_n^{(2)}(x)}{2} \right| = \Delta(x), \end{equation}

тобто багаточлен

\begin{equation} \frac{Q_n^{(1)}(x) + Q_n^{(2)}(x)}{2} \end{equation}

також є БНРН. Нехай $x_0, x_1, \ldots, x_m$ — відповідні йому точки чебишовського альтернансу.

Це означає, що

\begin{equation} \left| \frac{Q_n^{(1)}(x_i) + Q_n^{(2)}(x_i)}{2} - f(x_i) \right| = \Delta(f), \end{equation}

або

\begin{equation} \label{eq:8.2.2} \left( Q_n^{(1)} (x_i) - f(x_i) \right)+ \left( Q_n^{(2)} (x_i) - f (x_i) \right) = 2 \Delta (f). \end{equation}

Оскільки $\left\vert Q_n^{(k)} (x_i) - f(x_i) \right\vert \le \Delta(f)$, $k = 1,2$, то \eqref{eq:8.2.2} можливе лише у тому випадку, коли

\begin{equation} Q_n^{(1)} (x_i) - f(x_i) = Q_n^{(2)} (x_i) - f(x_i), \end{equation}

для усіх $i = \overline{0, n + 1}$.

Звідки випливає, що $Q_n^{(1)}(x) = Q_n^{(2)}(x)$, а це суперечить початковому припущенню. $\square$

8.3. Приклади побудови БНРН

Література

• Бахвалов, Жидков, Кобельков, стор. 181–187: pdf

• Волков, стор. 81–90: pdf

Скінченого алгоритму побудови БНРН для довільної функції не існує. Є ітераційний [ЛМС, 73–79]. Але в деяких випадках можна побудувати БНРН за теоремою Чебишова.

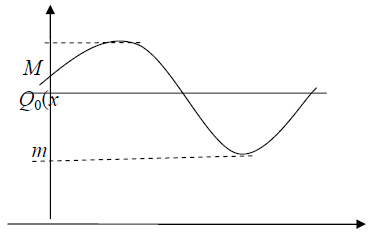
1. Потрібно наблизити багаточленом нульового степеня.

   

   Нехай $M = \Max_{[a, b]} f(x) = f(x_0)$, $m = \Min_{[a,b]} f(x) = f(x_1)$, тоді $Q_0(x)$ — БНРН має вигляд (див. рис. 11):

   \begin{equation} Q_0(x) = \frac{M + m}{2}, \end{equation}

   де $\Delta(x_0) = \frac{M + m}{2}$, а $x_0$, $x_1$ — точки чебишовського альтернансу.

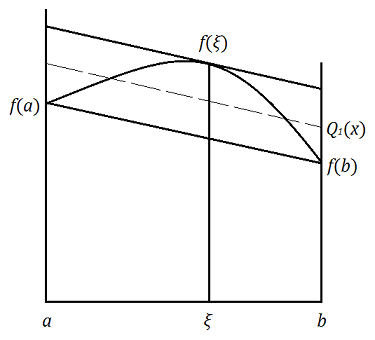
2. Опукла функція $f(x) \in C([a,b])$ наближається багаточленом першого степеня

   \begin{equation} Q_1(x) = c_0 + c_1 x. \end{equation}

   Оскільки $f(x)$ опукла, то різниця $f(x) - (c_0 + c_1 x)$ може мати лише одну внутрішню точку екстремуму. Тому точки $a$, $b$ є точками чебишовського альтернансу. Нехай $\xi$ третя — точка чебишовського альтернансу. Згідно з теоремою Чебишова, маємо систему:

   $$\begin{equation} \left\{ \begin{aligned} f(a) - c_0 - c_1 a &= \alpha \Delta(f), \newline f(\xi) - c_0 - c_1 \xi &= - \alpha \Delta(f), \newline f(b) - c_0 - c_1 b &= \alpha \Delta(f). \end{aligned} \right. \end{equation}$$

   Звідси $f(b) - f (a) = c_1 (b - a)$ та $c_1 = \frac{f(b) - f(a)}{b - a}$.

   Цю систему треба замкнути, використавши ще одне рівняння з умови: точка $\xi$ є точкою екстремуму різниці $f(x) - (c_0 + c_1 x)$. Тому для диференційованої функції $f(x)$ для визначення $\xi$ маємо рівняння (дотична і січна паралельні):

   \begin{equation} f’(\xi) = c_1 = \frac{f(b) - f(a)}{b - a} \end{equation}

   

   Геометрично ця процедура виглядає наступним чином (див. рис. 12). Проводимо січну через точки $(a, f (a))$, $(b, f (b))$. Для неї тангенс кута дорівнює $c_1$. Проводимо паралельну їй дотичну до кривої $y = f(x)$, а потім пряму, рівновіддалену від січної та дотичної, яка і буде графіком $Q_1(x)$. При цьому $x_0 = a$, $x_1 = \xi$, $x_2 = b$.

3. Потрібно наблизити $f(x) = x^{n + 1}$, $x \in [-1,1]$ багаточленом степеня $n$: $Q_n^0(x)$. Введемо

   \begin{equation} \overline P_{n + 1}(x) = x^{n + 1} - Q_n(x) = x^{n + 1} - a_1 x^n - \ldots \end{equation}

   Далі

   $$\begin{equation} \begin{aligned} \Delta(f) &= \Inf_{Q_n(x)} \left\| x^{n + 1} - Q_n^0(x) \right\|_C = \newline &= \Inf_{\overline{P}_{n + 1}} \left\| \overline{P}_{n + 1} - 0 \right\|_C = \newline &= \left\| \overline{T}_{n + 1}(x) \right\|. \end{aligned} \end{equation}$$

   Звідси

   $$\begin{equation} x^{n + 1} - Q_n^0(x) = \overline T_{n + 1}(x), \end{equation}$$

   або

   $$\begin{equation} Q_n^0(x) = x^{n + 1} - \overline T_{n + 1}(x). \end{equation}$$

   Задача 25: Для прикладу 3 вказати точки чебишовського альтернансу $\{x_i\}$, $i = \overline{0, n + 1}$.

4. Потрібно наблизити $f(x) = P_{n + 1}(x) = a_0 + \ldots + a_{n + 1} x^{n + 1}$, $a_{n + 1} \ne 0$, $x \in [a, b]$ БНРН степеня $n$. Запишімо його у вигляді:

   \begin{equation} Q_n^0(x) = P_{n + 1}(x) - a_{n + 1}(x) \overline T_{n + 1}^{[a, b]} \end{equation}

   де $\overline T_{n + 1}^{[a, b]}(x)$ — нормований багаточлен Чебишова на проміжку $x \in [a,b]$.

   Дійсно це БНРН: вираз у правій частині є багаточленом степеня $n$, оскільки коефіцієнт при $x^{n + 1}$ дорівнює нулю, а його нулі

   \begin{equation} x_k = \frac{b + a}{2} + \frac{b - a}{2} \cdot t_k, \end{equation}

   де

   \begin{equation} t_k = \cos \left( \frac{(2 k + 1) \pi}{2 (n + 1)} \right), \end{equation}

   для $k = \overline{0,n}$ є точками чебишевського альтернасу для $Q_n^0(x)$.

   Задача 26: Показати, що для $f(x)$ парної (непарної) функції БНРН це багаточлен по парних (непарних) степенях $x$.

5. Телескопічний метод. Дуже часто БНРН точно знайти не вдається. В таких випадках шукається багаточлен, близький до нього. Бажано щоб цей багаточлен був невисокого степеня (менше арифметичних операцій на його обчислення) Спочатку будують такий багаточлен

   \begin{equation} P_n(x) = \Sum_{j = 0}^n a_j x^j, \end{equation}

   щоб відхилення від $f(x)$ була достатньо малою. (наприклад меншою за $\varepsilon / 2$).

   Можна це зробити, наприклад, за формулою Тейлора. Потім наближають багаточлен $P_n(x)$ багаточленом найкращого рівномірного наближення $P_{n-1}(x)$ (за алгоритмом п. 4; для простоти $x \in [-1,1]$):

   \begin{equation} P_{n - 1}(x) = P_n(x) - a_n T_n(x) 2^{1 - n}. \end{equation}

   Оскільки $\vert T_n(x) \vert \le 1$ на відрізку $[-1, 1]$, то

   \begin{equation} | P_{n - 1}(x) - P_n(x) | \le |a_n| \cdot 2^{1 - n}. \end{equation}

   Далі наближають багаточлен $P_{n-1}(x)$ багаточленом найкращого рівномірного наближення $P_{n - 2}(x)$ і т. д. Пониження степеня продовжується до тих пір, поки сумарна похибка від таких послідовних апроксимацій залишається меншою за задане мале число $\varepsilon$.

8.4. Найкраще середньоквадратичне наближення

Література:

• БЖК, стор. 156–166;

• ЛМС, стор. 53–58.

Наблизимо функцію $f(x) \in H$ з гільбертового простору $H$ функціями із скінченно-вимірного підпростору $M_n$ простору $H$. Тут $H$ — гільбертів простір із скалярним добутком $\langle u, r \rangle$, норма і відстань для якого визначаються формулами:

\begin{equation} |u| = \sqrt{\langle u, u \rangle}, \quad \Delta(u, v) = |u - v|. \end{equation}

Побудуємо

\begin{equation} \label{eq:8.4.1} u = \Sum_{i=0}^n c_i \varphi_i \in M_n \subset H, \end{equation}

де $\{\varphi_i\}\void_{i=0}^\infty$ — лінійно-незалежна система елементів з $H$.

Означення: Елементом найкращого середньоквадратичного наближення (в подальшому ЕНСКН) називатимемо $\Phi_0$ такий, що

\begin{equation} |f - \Phi_0| = \sqrt{\langle f - \Phi_0, f - \Phi_0 \rangle} = \Inf_{\Phi \in M_n} |f - \Phi|. \end{equation}

Теорема 1: Нехай $f \in H$, $\Phi_0 \in M_n$ — елемент найкращого середньоквадратичного наближення, тобто

\begin{equation} |f - \Phi_0| = \Inf_{\Phi \in M_n} |f - \Phi|, \end{equation}

тоді

\begin{equation} \label{eq:8.4.2} \forall \Phi \in M_n: \quad \langle f - \Phi_0, \Phi \rangle = 0. \end{equation}

Доведення:

Нехай \eqref{eq:8.4.2} не виконується, тобто $\exists \Phi_1 \in M_n$:

\begin{equation} \langle f - \Phi_0, \phi_1 \rangle = \alpha \ne 0. \end{equation}

Без обмеження загальності можемо вважати, що $\|\Phi_1\| = 1$.

Побудуємо $\Phi_2 = \Phi_0 + \alpha \Phi_1$, тоді

\begin{equation} \begin{aligned} |f - \Phi_2|^2 &= \langle f - \Phi_2, f - \Phi_2 \rangle = \newline &= |f - \Phi_0|^2 - \alpha^2 < |f - \Phi_0|^2. \end{aligned} \end{equation}

Отже, елемент $\Phi_2$ кращий за елемент найкращого середньоквадратичного наближення $\Phi_0$. А це суперечність. $\square$

Наслідок: $f = \Phi_0 + \nu$, де $\Phi_0 \in M_n$, а $\nu \perp M_n$ (поправка $\nu$ — з ортогонального доповнення до $M_n$).

Знайти ЕНСКН

\begin{equation} \label{eq:8.4.3} \Phi_0 = \Sum_{i = 0}^n c_i \varphi_i \end{equation}

означає знайти коефіцієнти $c_i$.

Для виконання \eqref{eq:8.4.2} достатньо, щоб

\begin{equation} \label{eq:8.4.4} \langle f - \Phi_0, \varphi_k \rangle = 0, \quad k = \overline{0, n}. \end{equation}

Підставимо \eqref{eq:8.4.3} у формулу \eqref{eq:8.4.4}:

\begin{equation} \langle f - \Sum_{i = 0}^n c_i \varphi_i, \varphi_k \rangle = 0. \end{equation}

Таким чином маємо СЛАР для $c_i$:

\begin{equation} \label{eq:8.4.5} \Sum_{i=0}^n c_i \langle \varphi_i, \varphi_k \rangle = \langle f, \varphi_k \rangle ,\quad k = \overline{0, n}. \end{equation}

З теореми $1$ витікає лише достатність умов \eqref{eq:8.4.5} для знаходження коефіцієнтів $c_i$. Розглянемо задачу

\begin{equation} |f - \Phi_0| = \Inf_{\Phi \in M_n} |f - \Phi|, \end{equation}

як задачу мінімізації функції багатьох змінних:

\begin{equation} F(a_0, \ldots, a_n) = |f - \Phi|^2 = \left| f - \Sum_{i=0}^n a_i \varphi_i \right|^2 \to \min. \end{equation}

Умови мінімуму цієї функції приводять до \eqref{eq:8.4.5}.

Задача 27: Показати, що для коефіцієнтів $c_i$ елемента найкращого середньо-квадратичного наближення умови \eqref{eq:8.4.5} є необхідними та достатніми.

Матриця СЛАР \eqref{eq:8.4.5} складається з елементів $g_{ik}=\langle \varphi_i, \varphi_k\rangle$, тобто це матриця Грамма: $G = (g_{ik})^n_{i,k=0}$. Оскільки це матриця Грамма лінійно-незалежної системи, то $\det G \ne 0$det, що ще раз доводить існування та єдиність ЕНСКН. Оскільки $G^\intercal = G$, то для розв’язку цієї системи використовують метод квадратних коренів.

Якщо взяти $x \in [0,1]$ та $\varphi_i(x) = x^i$, $i = \overline{0, n}$, $H = L_2(0,1)$, то

\begin{equation} g_{ik} = \Int_0^1 x^i x^k \diff x = \frac{1}{i + k + 1}, \quad i, k = \overline{0, n}. \end{equation}

Це матриця Гілберта, яка є погано обумовленою: $\text{cond} G \approx 10^7$, $n = 6$. Праві частини

\begin{equation} f_k = \langle f, \varphi_k \rangle = \Int_0^1 f(x_i) x^k \diff x \end{equation}

як правило, обчислюються наближено, тому похибки обчислення $c_i$ можуть бути великими.

Що робити? Якщо вибирати систему $\{\varphi_i\}^\infty_{i=0}$ ортонормованою, тобто

\begin{equation} \langle \varphi_i, \varphi_k \rangle = \delta_{ik} = \begin{cases} 1, & i = k, \newline 0, & i \ne k, \end{cases} \end{equation}

то система \eqref{eq:8.4.5} має явний розв’язок

\begin{equation} \label{eq:8.4.6} \Phi_0 = \Sum_{i=0}^n \langle f, \varphi_i \rangle \cdot \varphi_i. \end{equation}

Якщо $\{\varphi_i\}$ — повна ортонормована система, то довільну функцію можна представити у вигляді ряду Фур’є:

\begin{equation} f = \Sum_{i=0}^\infty \langle f, \varphi_i \rangle \cdot \varphi_i, \end{equation}

і

\begin{equation} f - \Phi_0 = \Sum_{i = n + 1}^\infty c_i \varphi_i = \nu \end{equation}

— залишок (похибка). Таким чином ЕНСКН є відрізком ряду Фур’є. Далі

\begin{equation} \begin{aligned} |f - \Phi_0|^2 &= \langle f - \Phi_0, f - \Phi_0 \rangle = \newline &= |f|^2 - 2 \langle f, \Phi_0 \rangle + |\Phi_0|^2 = \newline &= |f|^2 - 2 |\Phi_0|^2 - 2 \langle \nu, \Phi_0\rangle + |\Phi_0| = \newline &= |f|^2 - |\Phi_0|^2 = \newline &= \Sum_{i = 0}^\infty c_i^2 - \Sum_{i=0}^n c_i^2 = \newline &= \Sum_{i = n + 1}^\infty c_i^2 \xrightarrow[n \to \infty]{} 0. \end{aligned} \end{equation}

Останнє випливає з відповідної теореми математичного аналізу. Таким чином, якщо $\{\varphi_i\}^\infty_{i=0}$ — повна ортонормована система, то

\begin{align} \Sum_{i = n + 1}^\infty c_i^2 &\xrightarrow[n \to \infty]{} 0, \newline \Phi_0^{(n)} &\xrightarrow[n \to \infty]{} f, \end{align}

Значить вірна

Теорема 2: В гільбертовому просторі $H$ послідовність ЕНСКН $\left\{\Phi_0^{(n)}\right\}$ по повній ортонормованій системі $\{\varphi_i\}^\infty_{i=0}$ збігається до $f$ .

Зауваження 1: Відхилення можна обчислити за формулою:

\begin{equation} \begin{aligned} \Delta^2(f) &= |f - \Phi_0|^2 = \newline &= |f|^2 - 2 \langle f, \Phi_0 \rangle + |\Phi_0|^2 = \newline &= |f|^2 - |\Phi_0|^2 = |f|^2 - \Sum_{i = 0}^n c_i^2. \end{aligned} \end{equation}

Якщо $\{\varphi_i\}^\infty_{i=0}$ — ортогональна система, але не нормована, тобто $\langle \varphi_i, \varphi_k \rangle = \delta_{ik} \|\varphi_i\|^2$, то

\begin{align} c_i &= \frac{\langle f, \varphi_i \rangle}{|\varphi_i|^2}, \newline \Phi_0 &= \Sum_{i = 0}^n \frac{\langle f, \varphi_i \rangle}{|\varphi_i|^2} \cdot \varphi_i, \newline |f - \Phi_0|^2 &= |f|^2 - \Sum_{i = 0}^n \frac{c_i^2}{|\varphi_i|^2}. \end{align}

Для функції $f(x)$, щоб побудувати ЕНСКН покладемо $H = L_{2,\alpha}([a,b])$, в якому скалярний добуток виберемо наступним чином

\begin{equation} \langle u, v \rangle = \Int_a^b u(x) v(x) \diff \alpha(x), \end{equation}

де $\alpha(x)$ — зростаюча функція. Можливі випадки:

1. $\alpha(x) \in C^1([a,b])$, тоді $\diff \alpha(x) = \rho(x) \diff x > 0$ та

   \begin{equation} \langle u, v \rangle = \Int_a^b \rho(x) u(x) v(x) \diff x. \end{equation}

2. $\alpha(x)$ — функція стрибків, $\alpha(x) = \alpha(x_k - 0)$, де $x_{k-1} \le x \le x_k$, $k = \overline{1,n}$. Якщо ввести $\rho_k = \alpha(x_k + 0) - \alpha(x_k - 0)$, то

   \begin{equation} \langle u, v \rangle = \Sum_{k = 1}^n \rho_k u(x_k) v(x_k). \end{equation}

Перший вибір $\alpha(x)$ використовується при апроксимації функцій неперервного аргументу, а другий — для табличних функцій.

8.5. Системи ортогональних функцій

Література:

• БЖК, стор. 19–102;

• ЛМС, стор. 388–382.

Як вибирати ортонормальну або ортогональну систему функцій $\{\varphi_i\}^\infty_{i = 0}$?

Розглянемо деякі з найбільш вживаних таких систем.

1. Якщо $H = L_2([-1,1])$; $\rho \equiv 1$ (ваговий множник), то $\varphi_i(x) = L_i(x)$ — система багаточленів Лежандра, які мають вигляд

   \begin{equation} L_n(x) = \frac{1}{2^n n!} \cdot \frac{\diff^n}{\diff x^n } \cdot (x^2 - 1)^n. \end{equation}

   Використовують також рекурентні формули

   \begin{equation} (n + 1) L_{n + 1}(x) = (2 n + 1) x L_n(x) - n L_{n - 1}(x), \end{equation}

   до яких додаємо умови

   \begin{equation} L_0(x) = 1, \quad L_1(x) = x. \end{equation}

   Це ортогональна система в тому сенсі, що

   \begin{equation} \langle L_i, L_k \rangle = \Int_{-1}^1 L_i(x) L_k(x) \diff x = \delta_{ik} |L_i(x)|^2, \end{equation}

   де $\|L_i(x)\|^2 = \frac{2}{2 i + 1}$ і тому $c_i = \frac{\langle f, L_i \rangle}{\|L_i\|^2} = \frac{2 i + 1}{2} \langle f, L_i \rangle$.

   Зауваження: Якщо потрібно побудувати наближення на довільному проміжку $(a, b)$, то бажано перейти до проміжку $(-1, 1)$, тобто по $f(x)$ на $[a, b]$ побудувати $f(t)$ з $t \in [-1, 1]$ заміною $x = A t + B$, $t = \alpha x + \beta$ та для побудови багаточлена НСКН для $f(t)$ використати багаточлени Лежандра $L_i(t)$.

   Можна робити навпаки — систему багаточленів перевести з $[a, b]$ на $[-1, 1]$, але це вимагає більше обчислень і процес побудови ЕНСКН складніше.

2. Якщо $H = L_{2, \rho} ([-1,1])$, $\rho(x) = 1 / \sqrt{1 - x^2}$, скалярний добуток

   \begin{equation} \langle u, v \rangle = \Int_{-1}^1 \frac{u(x) v(x)}{\sqrt{1 - x^2}} \diff x \end{equation}

   (це невласні інтеграли другого роду), то $\varphi_i(x) = T_i(x)$, де $\{T_i(x)\}$ — система ортогональних багаточленів Чебишова 1-го роду, які мають вигляд

   \begin{equation} T_n(x) = \cos(n \arccos(x)). \end{equation}

   Рекурентна формула для цих багаточленів:

   \begin{equation} T_{n + 1}(x) = 2 x T_n(x) - T_{n - 1}(x), \end{equation}

   до якої додаємо умови $T_0 = 1$, $T_1 = x$.

   Для цієї системи

   \begin{equation} |T_n|^2 = \begin{cases} \pi, & n = 0, \newline \pi / 2, & n = 1, 2, \ldots \end{cases} \end{equation}

3. $H$ гільбертів простір з ваговим множником $\rho(x) = (1 - x)^\alpha (1 + x)^\beta$. Система $\varphi_i(x) = P_n^{(\alpha, \beta)}(x)$ — багаточленів Якобі, $\alpha, \beta > -1$ ($\alpha$, $\beta$ — числові параметри) ортогональна в сенсі скалярного добутку

   \begin{equation} \langle u, v \rangle = \Int_{-1}^1 (1 - a)^\alpha (1 + x)^\beta u(x) v(x) \diff x. \end{equation}

   Ця система є узагальненням випадків 1. та 2.

   Диференціальна формула для багаточленів:

   \begin{equation} P_n^{(\alpha, \beta)}(x) = \frac{(-1)^n}{2^n n!} (1 - x)^{-\alpha} (1 + x)^{-\beta} \frac{\diff^n}{\diff x^n} \left( (1 - x)^{n + \alpha} (1 + x)^{n + \beta} \right). \end{equation}

   Рекурентна формула:

   \begin{align} & 2 (n + 1) (n + \alpha + \beta + 1) (2 n + \alpha + \beta) P_{n + 1}^{(\alpha, \beta)}(x) = \newline & \quad = (2 n + \alpha + \beta + 1) ( (2 b + \alpha + \beta) (2 n + \alpha + \beta + 2) x + \alpha^2 - \beta^2) P_n^{(\alpha, \beta)}(x) - \newline & \qquad - 2 (n + \alpha) (n + \beta) (2 n + \alpha + \beta + 2) P_{n - 1}^{(\alpha, \beta)}(x), \end{align}

   де $P_0^{(\alpha, \beta)} = 1$, $P_{-1}^{(\alpha, \beta)} = 0$, і

   \begin{equation} \left| P_n^{(\alpha, \beta)} \right|^2 = \frac{2^{\alpha + \beta + 1} \Gamma(\alpha + n + 1) \Gamma(\beta + n + 1)}{n! (\alpha + \beta + 2 n + 1) \Gamma(\alpha + \beta + n + 1)}, \end{equation}

   та

   \begin{equation} \Gamma(z) = \Int_0^\infty e^{-t} t^{z - 1} \diff t, \end{equation}

   а $\Gamma(z + 1) = z \cdot \Gamma(z)$, $\Gamma(n + 1) = n!$.

   Коли $\alpha = \beta = 0$: $P_n^{(0, 0)}(x) = L_n(x)$, а для $\alpha = \beta = - 1 / 2$: $P_n^{(-1/2, -1/2)}(x) = T_n(x)$.

4. $H = L_{2, \rho} ([0, \infty))$, $\rho(x) = x^\alpha e^{-x}$, $\alpha > -1$.

   Цьому ваговому множнику відповідає система багаточленів Лагерра $\varphi_i(x) = L_i^\alpha(x)$, які задаються диференціальною формулою:

   \begin{equation} L_n^\alpha(x) = (-1)^n x^{-\alpha} e^x \frac{\diff^n}{\diff x^n} \left(x^{\alpha + n} e^{-x}\right) \end{equation}

   або в рекурентній формі

   \begin{equation} (n + 1) L_{n + 1}^\alpha = (2 n + \alpha + 1 - x) L_n^\alpha - (n + \alpha) L_{n - 1}^\alpha, \end{equation}

   де $L_0^\alpha = 1$, $L_{-1}^\alpha = 0$ та з нормою $\|L_n^\alpha\|^2 = n! \cdot \Gamma(\alpha + n + 1)$.

5. $H = L_{2,\alpha}((-\infty,\infty))$, $\rho(x) = e^{-x^2}$. Систему ортогональних функцій вибираємо як систему багаточленів Ерміта $\varphi_i(x) = H_i(x)$, які задаються диференціальною формулою:

   \begin{equation} H_n(x) = (-1)^n e^{x^2} \frac{\diff^n}{\diff x^n} e^{-x^2}, \end{equation}

   або в рекурентній формі

   \begin{equation} H_{n + 1}(x) = 2 x H_n(x) - 2 n H_{n - 1}(x) \end{equation}

   де $H_0 = 1$, $H_{-1} = 0$ та $\|H_n\|^2 = 2^n n! \sqrt{\pi}$.

6. $H = L_2([0,2\pi])$, $\rho(x) \equiv 1$, $f(x) = f (x + 2\pi)$. $f(x)$ — $2\pi$-періодичні функції. За систему ортонормованих функцій вибираємо тригонометричну систему

   \begin{align} \varphi_0(x) &= \frac{1}{\sqrt{2\pi}}, \newline \varphi_{2 k - 1}(x) &= \frac{\cos(k x)}{\sqrt{\pi}}, \newline \varphi_{2 k}(x) &= \frac{\sin(k x)}{\sqrt{\pi}}. \end{align}

   Елемент найкращого середньоквадратичного наближення представляє собою тригонометричний багаточлен

   \begin{equation} \Phi_0(x) \equiv T_n(x) = \frac{a_0}{2} + \Sum_{k = 1}^n (a_k \cos(k x) + b_k \sin(k x)), \end{equation}

   формули для обчислення цих коефіцієнтів наведені в наступному пункті.

7. Якщо потрібно апроксимувати табличну функцію, то $H = \ell_2$, $x_i = i$, $i = \overline{0, N}$,

   \begin{equation} \langle u, v \rangle = \frac{1}{N + 1} \Sum_{i = 0}^N u_i v_i, \end{equation}

   і за систему ортогональних функцій вибираємо наступну систему багаточленів: $\varphi_k(x) = p_k^{(N)}(x)$, $k = \overline{0,m}$ ($m \le N$) — систему багаточленів Чебишова дискретного аргументу, які задається формулою

   \begin{equation} p_k^{(N)}(x) = \Sum_{j = 0}^k \frac{(-1)^j C_k^j C_{k + j}^j}{N^{(j)}} \cdot x^{(j)} \end{equation}

   де $x^{(j)} = x (x - 1) \ldots (x - j + 1)$ — факторіальний багаточлен; $C_k^j$ — число сполук.

   Рекурентна формула:

   \begin{equation} \frac{(m + 1) (N - m)}{2 (2 m + 1)} \cdot p_{m + 1}^{(N)} = \left( \frac{N}{2} - x \right) p_m^{(N)} - \frac{m (N + m + 1)}{2 (2 m + 1)} \cdot p_{m - 1}^{(N)}, \end{equation}

   з початковими значеннями $p_0^{(N)} = 1$, $p_{-1}^{(N)} = 0$.

   Наприклад $p_1^{(N)} = 1 - \frac{2 x}{N}$, $p_2^{(N)} = 1 - \frac{6 x}{N} + \frac{6 x^2}{N (N - 1)}$.

   У випадку, якщо задані вузли $t_i = t_0 + i h$, $i = \overline{0, N}$, то робимо заміну $x_i = \frac{t_i - t_0}{h} = i$.

8.6. Середньоквадратичне наближення періодичних функцій

Література:

• ЛМС, стор. 60–61;

• БЖК, стор. 166–182.

Нехай маємо періодичну функцію $f(x)$ неперервного аргументу, з періодом $T = 2\pi$, тобто $f(x + 2\pi) = f(x)$. В просторі $H_2 = L_2([0,2\pi])$ визначений скалярний добуток:

\begin{equation} \langle u, v \rangle = \Int_0^{2 \pi} u(x) v(x) \diff x \end{equation}

В якості системи лінійно-незалежних функцій $\{\varphi_i\}$ виберемо тригонометричну систему функцій:

\begin{equation} \varphi_0(x) = 1; \quad \varphi_{2 k - 1}(x) = \cos(k x); \quad \varphi_{2 k}(x) = \sin(k x), \end{equation}

для $k = 1, 2, \ldots$, яка є повною нормованою системою в $L_2([0,2\pi])$.

Будемо шукати $\Phi(x)$ у вигляді тригонометричного багаточлена

\begin{equation} \label{eq:8.6.1} \Phi_0(x) \equiv T_n(x) = \frac{a_0}{2} + \Sum_{k = 1}^n (a_k \cos(k x) + b_k \sin(k x)), \end{equation}

За теорією найкращого середньоквадратичного наближення коефіцієнти обчислюємо за формулами:

\begin{equation} \label{eq:8.6.2} \left\{ \begin{aligned} a_0 &= \langle f, \varphi_0\rangle = \frac{1}{2\pi} \Int_0^{2\pi} f(x) \diff x, \newline a_k &= \langle f, \varphi_{2 k - 1} \rangle = \frac{1}{\pi} \Int_0^{2 \pi} f(x) \cos (k x) \diff x, \newline b_k &= \langle f, \varphi_{2 k} \rangle = \frac{1}{\pi} \Int_0^{2 \pi} f(x) \sin (k x) \diff x. \end{aligned} \right. \end{equation}

Відхилення:

\begin{equation} \Delta^2(f) = |f|^2 - \left( 2 \pi a_0^2 + \Sum_{k = 1}^n \pi (a_k^2 + b_k^2) \right). \end{equation}

Тепер нехай функція $f(x)$ задана таблично: $f_i = f(x_i)$, $i = \overline{1, N}$. Тригонометрична система $\varphi_0(x)$, $\varphi_{2k - 1}(x)$, $\varphi_{2k}(x)$ — ортогональна в $H = L_2(\omega)$ для $\omega = \{ x_i = \pi i / N, i = \overline{1,n}\}$ в сенсі скалярного добутку

\begin{equation} \langle u, v \rangle = \frac{1}{N} \Sum_{i = 1}^{N} u_i v_i, \quad u_i = u(x_i). \end{equation}

Тоді

\begin{equation} \label{eq:8.6.3} \left\{ \begin{aligned} a_0 &= \frac{1}{N} \Sum_{i = 1}^{N} f_i, \newline a_k &= \frac{2}{N} \Sum_{i = 1}^{N} f_i \cos (k x_i), \newline b_k &= \frac{2}{N} \Sum_{i = 1}^{N} f_i \sin (k x_i), \newline \end{aligned} \right. \end{equation}

Це формули Бесселя. В формулі \eqref{eq:8.6.1}: $\Phi(x) \equiv T_n(x)$ (тобто багаточлен той же), але коефіцієнти визначаємо за формулою $(105)$.

Зауваження: Як правило кількість даних значень $N \gg 2n + 1$. Але якщо $N = 2 n + 1$, то $n =\frac{N - 1}{2}$ і $N$ — непарне. При цьому $T_{\frac{N - 1}{2}}(x)$ — БНСКН і звідси

\begin{equation} \Delta^2(f) = \left| f(x) - T_{\frac{N - 1}{2}}(x) \right|^2 = \frac{1}{N} \Sum_{i = 1}^{N} \left(f(x_i) - T_{\frac{N - 1}{2}}(x) \right)^2 \to \Inf_{a_k, b_k}. \end{equation}

Оскільки найменше значення відхилення $\Delta^2(f) = 0$, то тригонометричний багаточлен найкращого середньоквадратичного наближення співпадає з інтерполяційним тригонометричним багаточленом і

\begin{equation} T_{\frac{N - 1}{2}}(x) = f(x_i). \end{equation}

Для визначення коефіцієнтів $a_i$, $b_i$ за формулою Бесселя $(105)$ необхідна кількість операцій $Q = O(N^2)$. Існують алгоритми, які дозволяють обчислити за $Q = O(N \cdot \log (N))$ операцій. Це так званий алгоритм швидкого перетворення Фур’є. Якщо в $(105)$ існує група доданків, які рівні між собою, тобто число $N$ можна представити як $N = p_1 p_2$, то можна так вибрати сітку, що $Q = O(N \cdot \max(p_1, p_2))$. Якщо ж $N = n^m$, то $Q = O(N m) = O(N \log_2(N))$.

8.7. Метод найменших квадратів (МНК)

Література:

• ЛМС, стор. 61–65;

• В, стор. 88–93.

Нехай в результаті вимірювань функції $f(x)$ маємо таблицю значень:

\begin{equation} \label{eq:8.7.1} y_i \approx f(x_i), \quad i = \overline{1,N}, \quad x_i \in [a,b]. \end{equation}

За даними цієї таблиці треба побудувати аналітичну формулу $\Phi(x; a_0, a_1, \ldots, a_n)$ таку, що

\begin{equation} \label{eq:8.7.2} \Phi(x_i; a_0, a_1, \ldots, a_n) \approx y_i, \quad i = \overline{1,N}. \end{equation}

Виконувати це інтерполюванням тобто задавати

\begin{equation} \label{eq:8.7.3} \Phi(x_i; a_0, a_1, \ldots, a_n) = y_i, i = \overline{1,N} \end{equation}

нераціонально, бо $N \gg n$ і система перевизначена; її розв’язки як правило не існують. Вигляд функції $\Phi(x; a_0, a_1, \ldots, a_n)$ і число параметрів $a_i$ у деяких випадках відомі. В інших випадках вони визначаються за графіком, побудованим за відомими значеннями $f(x_i)$ так, щоб залежність \eqref{eq:8.7.2} була досить простою і добре відображала результати спостережень. Але такі міркування не дають змогу побудувати єдиний елемент та й ще найкращого наближення.

Тому визначають параметри $a_0, \ldots, a_n$ так, щоб у деякому розумінні всі рівняння системи \eqref{eq:8.7.2} одночасно задовольнялись з найменшою похибкою, наприклад, щоб виконувалося:

\begin{equation} \label{eq:8.7.4} I(a_0, \ldots, a_n) = \Sum_{i = 1}^{N} \left(y_i - \Phi(x_i; a_0, \ldots, a_n)\right)^2 \to \min. \end{equation}

Такий метод розв’язання системи \eqref{eq:8.7.2} і називають методом найменших квадратів, оскільки мінімізується сума квадратів відхилення $\Phi(x; a_0, a_1, \ldots, a_n)$ від значень $f(x_i)$.

Для реалізації мінімуму необхідно та достатньо виконання умов:

\begin{equation} \label{eq:8.7.5} \frac{\partial I}{\partial a_i} = 0, \quad i = \overline{0, n}, \end{equation}

Якщо $\Phi(x_i; a_0, \ldots, a_n)$ лінійно залежить від параметрів $a_0, \ldots, a_n$, тобто

\begin{equation} \label{eq:8.7.6} \Phi(x; a_0, \ldots a_n) = \Sum_{k = 0}^{n} a_k \varphi_k(x), \end{equation}

то з \eqref{eq:8.7.3} маємо СЛАР:

\begin{equation} \label{eq:8.7.7} \Sum_{k = 0}^{n} a_k \varphi_k(x_i) = y_i, \quad i = \overline{1, N}, \end{equation}

яку називають системою умовних рівнянь. Позначивши

\begin{align} C &= (\varphi_k(x_i))\void_{j = \overline{0, n}}^{i = \overline{1, N}}, \newline \vec a &= (a_0, \ldots, a_n)^\intercal, \newline \vec y &= (y_1, \ldots, y_N)^\intercal, \end{align}

маємо матричний запис СЛАР \eqref{eq:8.7.7}:

\begin{equation} \label{eq:8.7.8} C \vec a = \vec y. \end{equation}

Помноживши систему умовних рівнянь \eqref{eq:8.7.8} зліва на транспоновану до $C$ матрицю $C^\intercal$ отримаємо систему нормальних рівнянь

\begin{equation} \label{eq:8.7.9} C^\intercal C \vec a = C^\intercal \vec y, \end{equation}

де $G = A = C^\intercal C$, $\dim G = n + 1$, $G = (g_{ik})^n_{i, k = 0}$, а самі

\begin{equation} g_{ik} = \Sum_{j = 1}^{N} c_{ij}^\intercal c_{jk} = \Sum_{j = 1}^{N} c_{ji} c_{jk} = \Sum_{j = 1}^{N} \varphi_k(x_i) \varphi_j(x_i), \end{equation}

а

\begin{equation} C^\intercal \vec y = \left( \Sum_{i = 1}^{N} c_{ik} y_i \right)^n_{k = 0} \end{equation}

з якої власно і обчислюють невідомі коефіцієнти.

Покажемо, що МНК є методом знаходження ЕНСКН, якщо визначити скалярний добуток

\begin{equation} \langle u, v \rangle = \Sum_{i = 1}^{N} u(x_i) v(x_i). \end{equation}

Поставимо задачу знаходження ЕНСКН:

\begin{equation} \Delta(f, \Phi) = |f - \Phi|^2 = \langle f - \Phi, f - \Phi\rangle = \Sum_{i = 1}^{N} (y_i - \Phi(x_i, \vec a))^2 \to \inf. \end{equation}

За теорією середньоквадратичного наближення для цього необхідно, щоб коефіцієнти $a_0, \ldots, a_n$ знаходилися з системи:

\begin{equation} \Sum_{j = 0}^{n} a_k \langle \varphi_k, \varphi_j \rangle = \langle \varphi_k, f \rangle, \end{equation}

де $k = \overline{0, n}$, а це співпадає з \eqref{eq:8.7.9}.

Якщо відома інформація про обчислювальну похибку для значень $f(x_i)$: $\vert f(x_i) - y_i\vert < \varepsilon_i$, то вибирають такий скалярний добуток

\begin{equation} \langle u, v \rangle = \Sum_{i = 1}^{N} \rho_i u(x_i) v(x_i), \end{equation}

де $\rho_i = 1 / \varepsilon_i^2$,.

Нехай тепер $\Phi(x; a_0, \ldots, a_n)$ — нелінійна функція параметрів $a_0, \ldots, a_n$, наприклад:

\begin{equation} \Phi = a_0 e^{a_1 x} + a_2 e^{a_3 x} + \ldots, \end{equation}

або

\begin{equation} \Phi = a_0 \cos (a_1 x) + a_2 \sin (a_3 x) + \ldots \end{equation}

Складемо функціонал:

\begin{equation} \label{eq:8.7.10} S(a_0, \ldots, a_n) = \Sum_{i = 1}^{N} \rho_i (y_i - \Phi(x, \vec a))^2 \to \Int_a. \end{equation}

Оскільки тепер $\Phi(x; a_0, \ldots, a_n)$ нелінійна, то застосуємо метод лінеаризації.

Нехай відомі наближені значення $\vec a^{(0)} = \left(a_0^{(0)}, a_1^{(0)}, \ldots, a_n^{(0)}\right)$. Розкладемо $\Phi(x, \vec a)$ в околі $a^{(0)}$. Тоді отримаємо лінійне наближення до $\Phi(x, \vec a)$:

\begin{equation} \Phi(x, \vec a) \approx \Phi \left(x, \vec a^{(0)} \right) + \Sum_{k = 0}^{n} \frac{\partial \Phi}{\partial a_k} \left\langle x, \vec a^{(0)} \right\rangle \left( a_k - a_k^{(0)} \right). \end{equation}

Якщо ввести позначення

\begin{align} \vec x &= \vec a - \vec a^{(0)}, \newline y_i^\star &= y_i - \Phi \left( x, \vec a^{(0)} \right), \newline c_{i, k} &= \Phi_{a_k}’ \left( x_i, \vec a^{(0)} \right), \end{align}

то отримаємо систему умовних рівнянь відносно поправок до $\vec a^{(0)}$:

\begin{equation} \label{eq:8.7.11} C \vec z = \vec y^\star. \end{equation}

Замінимо її на систему нормальних рівнянь

\begin{equation} \label{eq:8.7.12} C^\intercal C \vec z = c^\intercal \vec y^\star. \end{equation}

Знайшовши $\vec z$, обчислюємо наступне наближення:$\vec a^{(1)} = \vec a^{(0)} + \vec z$. Цей процес можна продовжувати: на кожній ітерації знаходимо $\vec z^{(m)}$, $m = 0, 1, \ldots$ і уточнюємо наближення до $\vec a$: $\vec a^{(m)} = \vec a^{(m - 1)} + \vec z^{(m - 1)}$.

Умова припинення ітерацій

\begin{equation} \left| \vec z^{(m)} \right| = \sqrt{\Sum_{k = 0}^{n} \left(z_k^{(m)}\right)^2} < \varepsilon. \end{equation}

Важливим є вибір початкового наближення $\vec a^{(0)}$. З системи умовних рівнянь (нелінійної) виберемо деякі $n + 1$. Розв’язок цієї системи і дасть початкове наближення.

Для деяких простих нелінійних залежностей від невеликої кількості параметрів задачу можна ліанеризувати аналітично. Наприклад, розглянемо наближення даних алометричним законом

\begin{equation} y_i \approx f(x_i), \quad \Phi(x, A, \alpha) = A x^\alpha. \end{equation}

Система умовних рівнянь має вигляд:

\begin{equation} \Phi(x_i) = A x_i^\alpha = y_i, \quad i = \overline{1,N}. \end{equation}

Прологарифмуємо її:

\begin{equation} \psi(x_i) = \ln (\Phi(x_i)) = \ln (A) + \alpha \ln(x_i) = \ln(y_i), \quad i = \overline{1,N}. \end{equation}

Введемо $a = \ln (A)$. Тепер функція $\psi(x, a, \alpha)$ лінійна. Система умовних рівнянь відносно параметрів $a$ та $\alpha$ має вигляд:

\begin{equation} C \vec z = \vec b, \end{equation}

де $\vec z = (a, \alpha)$, $\vec b = (\ln(y_i))^N_{i = 1}$, а

\begin{equation} C = \begin{pmatrix} 1 & \ln (x_i) \newline \vdots & \vdots \newline 1 & \ln (x_n) \end{pmatrix} \end{equation}

Запишемо систему нормальних рівнянь для методу найменших квадратів:

\begin{equation} \label{eq:8.7.13} G = C^\intercal C = \begin{pmatrix} N & \Sum_{i = 1}^{N} \ln(x_i) \newline \Sum_{i = 1}^{N} \ln(x_i) & \Sum_{i = 1}^{N} (\ln(x_i))^2 \end{pmatrix}, \end{equation}

і

\begin{equation} \label{eq:8.7.14} C^\intercal \vec b = \begin{pmatrix} \Sum_{i = 1}^{N} \ln(y_i) \newline \Sum_{i = 1}^{N} \ln(x_i) \ln(y_i) \end{pmatrix}. \end{equation}

Розв’язавши систему \eqref{eq:8.7.13}–\eqref{eq:8.7.14}, знаходимо $\alpha$, та $A = \exp(a)$.

8.8. Згладжуючі сплайни

Література:

• Марчук Г. И., «Методы вычислительной математики», стор. 181–184.

Якщо значення в точках $x_i$ неточно $\tilde f_i = f_i + \varepsilon_i$, то застосовують згладжування. Для цього треба побудувати нову таблицю із згладженими значеннями $\bar f_i$.

Наведемо деякі прості формули згладжування:

1. $m = 1$:

   • $\bar f_i = \frac{1}{3} \left(\tilde f_{i - 1} + \tilde f_i + \tilde f_{i + 1}\right)$, $N = 3$;

   • $\bar f_i = \frac{1}{5} \left(\tilde f_{i - 2} + \ldots + \tilde f_{i + 2}\right)$, $N = 5$;

   • $\bar f_i = \frac{1}{2 k} \left(\tilde f_{i - k} + \ldots + \tilde f_{i + k}\right)$.

2. $m = 3$:

   • $\bar f_i = \frac{1}{3 \cdot 5} \left(- 3 \tilde f_{i - 2} + 12 \tilde f_{i - 1} + 17 \tilde f_i + 12 \tilde f_{i + 1} - 3 \tilde f_{i + 2}\right)$, $N = 5$.

Їх отримуємо в такий спосіб: до $\tilde f_i$ застосовуємо апроксимацію, будуємо багаточлен НСКН

\begin{equation} Q_m(x) = \Sum_{k = 0}^{m} c_k p_k^N (x), \end{equation}

де $p_k^N$ — система багаточленів Чебишова дискретного аргументу. Беремо значення $\bar f_i = Q_m(x_i)$, які приводять до наведених вище формул.

Але ці формули не дають гарантію, що в результаті ми отримаємо функцію, яка задовольняє умові $\vert \tilde f_i - f_i \vert < \varepsilon_i$.

Згладжуючі сплайни дають можливість побудувати наближення з заданою точністю. Нагадаємо деякі відомості про сплайни. Явний вигляд кубічного сплайна:

\begin{equation} \label{eq:8.8.1} \begin{aligned} s(x) &= m_{i - 1} \cdot \frac{(x_i - x)^3}{6 h_i} + m_i \cdot \frac{(x - x_{i - 1})^3}{6 h_i} + \newline & \quad + \left(f_{i - 1} - \frac{m_{i - 1} h_i^2}{6}\right) \cdot \frac{x_i - x}{h_i} + \newline & \quad + \left(f_i - \frac{m_i h_i^2}{6}\right) \cdot \frac{x - x_{i - 1}}{h_i}, \end{aligned} \end{equation}

для $x \in [x_{i-1}, x_i]$, де $h_i = x_i - x_{i - 1}$.

Тут $s(x_i) = f_i$, $i = \overline{0,n}$, а $m_i = s^{\prime\prime}(x_i)$ задовольняють систему:

\begin{equation} \label{eq:8.8.2} \left\{ \begin{aligned} & \frac{h_i m_{i - 1}}{6} + \frac{(h_i + h_{i + 1} m_i)}{3} + \frac{h_{i + 1} m_{i + 1}}{6} = \newline & \quad = \frac{f_{i + 1} - f_i}{h_{i + 1}} - \frac{f_i - f_{i - 1}}{h_i}, \quad i = \overline{1, n- 1} \newline & m_0 = m_n = 0. \end{aligned} \right. \end{equation}

В матричній формі ця система має вигляд

\begin{equation} \label{eq:8.8.3} A \vec m = H \vec f. \end{equation}

Тут

\begin{equation} \vec m = (m_1, \ldots, m_{n - 1})^\intercal, \quad \vec f = (f_0, \ldots, f_n)^\intercal, \end{equation}

а матриці

\begin{equation} A = \begin{pmatrix} \frac{h_1 + h_2}{3} & \frac{h_2}{6} & 0 & \cdots & 0 & 0 \newline \frac{h_2}{6} & \frac{h_2 + h_3}{3} & \frac{h_3}{6} & \cdots & 0 & 0 \newline \ddots & \ddots & \ddots & \ddots & \vdots & \vdots \newline \vdots & \ddots & \ddots & \ddots & \ddots & \vdots \newline 0 & \cdots & 0 & \frac{h_{n - 2}}{6} & \frac{h_{n - 2} + h_{n - 1}}{3} & \frac{h_{n - 1}}{6} \newline 0 & 0 & \cdots & 0 & \frac{h_{n - 1}}{6} & \frac{h_{n - 1} + h_n}{3} \newline 0 & 0 & 0 & \cdots & 0 & 1 \end{pmatrix} \end{equation}

і

\begin{equation} H = \begin{pmatrix} \frac{1}{h_1} & - \left( \frac{1}{h_1} + \frac{1}{h_2} \right) & \frac{1}{h_2} &0 & \cdots & 0 & 0 \newline 0 & \frac{1}{h_2} & - \left( \frac{1}{h_2} + \frac{1}{h_3} \right) & \frac{1}{h_3} & \cdots & 0 & 0 \newline \vdots & \vdots & \ddots & \ddots & \ddots & \vdots & \vdots \newline \vdots & \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \newline 0 & 0 & \cdots & 0 & \frac{1}{h_{n - 1}} & - \left( \frac{1}{h_{n - 1}} + \frac{1}{h_n} \right) & \frac{1}{h_n} \newline 0 & 0 & 0 & 0 & \cdots & 0 & 0 \end{pmatrix} \end{equation}

Кубічний інтерполяційний сплайн мінімізує функціонал:

\begin{equation} \label{eq:8.8.4} \Phi(u) = \Int_a^n (u^{\prime\prime}(x))^2 \diff x: \end{equation}

\begin{equation} \Phi(s) = \Int_{u \in U} \Phi(u), \end{equation}

де

\begin{equation} U = \left\{ u(x): u(x_i) = f_i, i = \overline{0, n}, u(x) \in W_2^2([a, b]) \right\}. \end{equation}

Введемо функціонал

\begin{equation} \Phi_1(u) = \Phi(u) + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - u(x_i) \right)^2. \end{equation}

Означення: Згладжуючим сплайном назвемо функцію $g$, яка є розв’язком задачі:

\begin{equation} \label{eq:8.8.5} \Phi_1(g) = \inf_{u \in W_2^2([a, b])} \Phi_1(u). \end{equation}

Перший доданок в $\Phi_1(u)$ дає мінімум «згину», другий — середньоквадратичне наближення до значень $\tilde f_i$. Покажемо, що $g$ є сплайном.

Нехай існує функція $g(x)$. Побудуємо кубічний сплайн такий, що $s(x_i) = g(x_i)$. З того, що $g(x)$ є розв’язком задачі \eqref{eq:8.8.5}, маємо $\Phi_1(s) \ge \Phi_1(g)$, а тоді

\begin{equation} \Int_a^b (s^{\prime\prime}(x))^2 \diff x + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - s(x_i) \right)^2 \ge \Int_a^b (g^{\prime\prime}(x))^2 \diff x + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - g(x_i) \right)^2 \end{equation}

Звідси $\Phi(s) \ge \Phi(g)$.

Оскільки кубічний інтерполяційний сплайн $s(x)$ мінімізує функціонал \eqref{eq:8.8.4} , то $\Phi(s) \le \Phi(g)$. Тому $\Phi(s) = \Phi(g)$. Звідки $s = g$.

Позначимо

\begin{equation} \label{eq:8.8.6} \mu_i = g(x_i), \quad i = \overline{0, n}, \end{equation}

Якби значення $\mu_i$ були б відомі, то для побудови $g$ достатньо було б розв’язати систему

\begin{equation} \label{eq:8.8.7} A \vec m = H \vec \mu \end{equation}

Підставимо $(144)$ та \eqref{eq:8.8.6} в $\Phi_1(g)$:

\begin{equation} \label{eq:8.8.8} \begin{aligned} \Phi_1(g) &= \Sum_{i = 1}^{n} \Int_{x_{i - 1}}^{x_i} \left(m_{i - 1} \cdot \frac{x_i - x}{h_i} + \newline & \quad + m_i \cdot \frac{x - x_{i - 1}}{h_i}\right)^2 \diff x + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - \mu_i \right)^2 = \newline &= \inf \Phi_1(u). \end{aligned} \end{equation}

Після перетворень маємо:

\begin{equation} \begin{aligned} \Phi_1(g) &= \Sum_{i = 1}^{n} \Int_{x_{i - 1}}^{x_i} \left(m_{i - 1} \cdot \frac{x_i - x}{h_i} + m_i \cdot \frac{x - x_{i - 1}}{h_i} \right)^2 \diff x + \newline & \quad + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - \mu_i \right)^2 = \newline &= \Sum_{i = 1}^{n} m_i \left(\frac{h_i m_{i - 1}}{6} + \frac{(h_i + h_{i + 1}) m_i}{3} + \frac{h_{i + 1} m_{i + 1}}{6} \right) \diff x + \newline & \quad + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - \mu_i \right)^2 = \newline &= \left\langle A \vec m, \vec m \right\rangle + \newline & \quad + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - \mu_i \right)^2. \end{aligned} \end{equation}

Задача 28: Показати, що для кубічного згладжуючого сплайну $g$ мають місце формули вище.

Оскільки $\Phi_1(g)$ представляє собою квадратичну функція відносно $\vec m = (m_0, \ldots, m_N)$, то необхідною і достатньою умовою мінімуму є

\begin{equation} \frac{\partial \Phi_1}{\partial \mu_1} = 0, \quad j = \overline{0,n}. \end{equation}

Знаходимо:

\begin{equation} \begin{aligned} \frac{\partial \Phi_1}{\partial \mu_j} &= \frac{\partial}{\partial \mu_j} \left\langle A \vec m, \vec m \right\rangle + 2 \rho_j \left( \mu_j - \tilde f_j \right) = \newline &= 2 \left\langle \frac{\partial}{\partial \mu_j} \left( A \vec m \right), \vec m \right\rangle + 2 \rho_j \left( \mu_j - \tilde f_j \right) = \newline &= 2 \left\langle \frac{\partial}{\partial m_j} \left( H \vec \mu\right), \vec m \right\rangle + 2 \rho_j \left( \mu_j - \tilde f_j \right) = \newline &= 2 \left\langle \frac{\partial \vec m}{\partial m_j}, H^\intercal \vec m \right\rangle + 2 \rho_j \left( \mu_j - \tilde f_j \right) = \newline &= 2 \left( H^\intercal \vec m \right)\void_j + 2 \rho_j \left( \mu_j - \tilde f_j \right) = 0. \end{aligned} \end{equation}

Отже, з умови мінімізації функціоналу

\begin{equation} \Phi_1(u) + \Int_a^b (u^{\prime\prime}(x))^2 \diff x + \Sum_{i = 0}^{n} \rho_i \left( \tilde f_i - u(x_i) \right)^2. \end{equation}

ми отримали таку систему рівнянь :

\begin{equation} \label{eq:8.8.9} 2 \left( H^\intercal \vec m\right)\void_i + 2 \rho_i (\mu_i - f_i) = 0, \end{equation}

де, як і раніше i $\mu_i$ — це невідомі значення згладжуючого сплайну:

\begin{equation} \mu_i = s(x_i), \quad m_i = s^{\prime\prime}(x_i). \end{equation}

Можна записати \eqref{eq:8.8.9} у матричному вигляді, якщо ввести матрицю $R = \diag \rho_i$:

\begin{equation} \label{eq:8.8.10} H^\intercal \vec m + R \vec \mu = R \vec f. \end{equation}

Тут $\vec f$ — вектор заданих значень функції.

Таким чином маємо для $\vec m$ та $\vec \mu$ дві системи \eqref{eq:8.8.7} і \eqref{eq:8.8.10}. Виключаючи $\vec \mu$ отримаємо таку систему лінійних рівнянь

\begin{equation} \label{eq:8.8.11} \left( A + H R^{-1} H^\intercal \right) \vec m = H \vec f. \end{equation}

Розв’язавши її, можемо обчислити

\begin{equation} \mu = \vec f - R^{-1} H^\intercal \vec m \end{equation}

і підставити знайдені значення $\mu_i$ та $m_i$ в формулу для сплайну

\begin{equation} \begin{aligned} g(x) &= m_{i - 1} \cdot \frac{(x_i - x)^3}{6 h_i} + m_i \cdot \frac{(x - x_{i - 1})^3}{6 h_i} + \newline & \quad + \left( \mu_{i - 1} - \frac{m_{i - 1} \cdot h_i^2}{6} \right) \cdot \frac{x_i - x}{h_i} + \newline & \quad + \left( \mu_i - \frac{m_i \cdot h_i^2}{6}\right) \cdot \frac{x - x_{i - 1}}{h_i}, \end{aligned} \end{equation}

Тепер звернемо увагу на матрицю системи \eqref{eq:8.8.10} :

\begin{equation} A’ = A + H R^{-1} H^\intercal. \end{equation}

Оскільки матриці $H$, $H^\intercal$ — трьохдіагональні, то матриця $H R^{-1} H^\intercal$ буде п’ятидіагональною, а тому п’ятидіагональною буде й $A'$.

Розв’язують зазвичай системи з такими матрицями наступним чином:

1. або методом квадратних коренів; для матриць із такою структурою цей метод має складність $Q = O(n m) = O(2 n) = O(n)$, оскільки в нашому випадку півширина діагональної смуги $m = 2$.

2. або методом п’ятидіагональної прогонки [Самарский А. А., Николаев С. Н., «Методы решения сеточных уравнений»], що також має складність $O(n)$.

Зауваження: $\rho_i$ вибирають так: $\rho_i = 1 / \varepsilon_i^2$.

Назад до лекцій

Назад на головну