Зміст:

• Синтаксичний аналіз

  • Стратегії виведення

  • Синтаксичні дерева

  • Власне аналіз

  • Синтез дерева за аналізом

  • Проблеми стратегії “зверху донизу”

• Контрольні запитання

Синтаксичний аналіз

Для визначення синтаксичної компоненти мови програмування використовують контекстно-вільні граматики (КС-граматики). На відміну від скінченно-автоматних граматик потужність класу КС-граматик достатня, щоб визначити майже всі так звані синтаксичні властивості мов програмування. Якщо цього недостатньо, то розглядають деякі спрощення у граматиках типу 2 або параметричні КC-граматики.

Звичайно, із синтаксичною компонентою мови програмування пов’язана семантична компонента. Тоді, якщо ми говоримо про семантику мови програмування, ми вимагаємо семантичної однозначності для кожної вірно написаної програми. За аналогією з семантикою, при описі синтаксичної компоненти мови програмування необхідно користуватися однозначними граматиками.

Граматика $G$ називається неоднозначною, якщо існує декілька варіантів виводу $\omega$ в $G$ $\left(\omega \in L(G)\right)$.

Приклад. Розглянемо таку граматику $G = \left\langle N, \Sigma, P, S\right\rangle$ з двома правилами у схемі $P$: $S \Rightarrow S + S$, і $S \Rightarrow a$. Покажемо, що для ланцюжка $\omega = a + a + a$ існує щонайменше два варіанти виводу:

1. $S \Rightarrow S + S \Rightarrow S + S + S \Rightarrow a + S + S \Rightarrow a + a + S \Rightarrow a + a + a$.

2. $S \Rightarrow S + S \Rightarrow a + S \Rightarrow a + S + S \Rightarrow a + a + S \Rightarrow a + a + a$.

Стратегії виведення

В теорії граматик розглядається декілька стратегій виведення ланцюжка $\omega$ в $G$. Визначимо дві стратегії, які будуть використані в подальшому.

Лівостороння стратегія виводу ланцюжка $\omega$ в $G$ — це послідовність кроків безпосереднього виводу, при якій на кожному кроку до уваги береться перший зліва направо нетермінал.

Правостороння стратегія виводу $\omega$ в $G$ протилежна лівосторонній стратегії.

З виводом $\omega$ в $G$ пов’язане синтаксичне дерево, яке визначає синтаксичну структуру програми.

Синтаксичні дерева

Синтаксичне дерево виведення $\omega$ в $G$ — це впорядковане дерево, корінь котрого позначено аксіомою, в проміжних вершинах знаходяться нетермінали, а на кроні — елементи з $\Sigma \cup \{\varepsilon\}$. Побудова синтаксичного дерева виведення $\omega$ в $G$ виконується покроково з урахуванням стратегії виводу $\omega$ в $G$.

Алгоритм [побудови синтаксичного дерева ланцюжка $\omega$ в граматиці $G$ урахуванням лівосторонньої стратегії виводу].

1. Будуємо корінь дерева та позначимо його аксіомою $S$.

2. В схемі $P$ граматики $G$ візьмемо правило виду $S \Rightarrow \alpha_1 \alpha_2 \ldots \alpha_p$, де $\alpha_i \in N \cup \Sigma \cup \{\varepsilon\}$ і побудуємо дерево висоти 1:

   

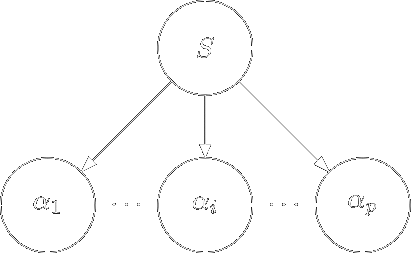
3. На кроні дерева, побудованого на попередньому кроці, візьмемо перший зліва направо нетермінал. Нехай це буде $\alpha_i$. Тоді в схемі $P$ виберемо правило виду $\alpha_i \Rightarrow \beta_1 \beta_2 \ldots \beta_l$, де $\beta_i \in N \cup \Sigma \cup \{\varepsilon\}$ і побудуємо наступне дерево:

   

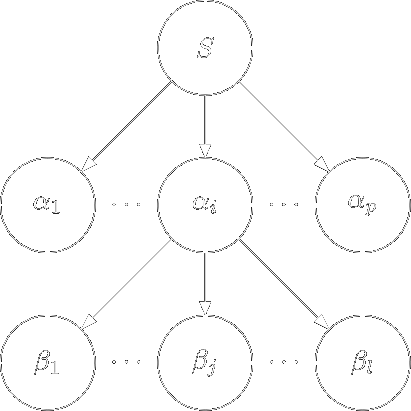
   Цей крок виконується доки на кроні дерева є елементи з $N$.

Зауважимо очевидні факти, що випливають з побудови синтаксичного дерева:

• крона дерева, зображеного на попередньому малюнку наступна: $\alpha_1 \alpha_2 \ldots \alpha_{i - 1} \beta_1 \beta_2 \ldots \beta_l \alpha_{i + 1} \ldots \alpha_p$;

• ланцюжок $\alpha_1 \alpha_2 \ldots \alpha_{i - 1} \in \Sigma^\star$ з крони — термінальний ланцюжок;

• для однозначної граматики $G$ існує лише одне синтаксичне дерево виводу $\omega$ в $G$.

Власне аналіз

Будемо говорити, що ланцюжок $\omega \in \Sigma^\star$, побудований на основі граматики $G$ $\left(\omega \in L(G)\right)$ проаналізований, якщо відоме одне з його дерев виводу.

Зафіксуємо послідовність номерів правил, які були використані під час побудови синтаксичного дерева виводу $\omega$ в $G$ з урахуванням стратегії виводу.

Лівостороннім аналізом $\pi$ ланцюжка $\omega \in L(G)$ будемо називати послідовність номерів правил, які були використані при лівосторонньому виводі $\omega$ в $G$.

Приклад: Для граматики $G = \left\langle N, \Sigma, P, S\right\rangle$ зі схемою $P$:

$$\begin{align} S &\Rightarrow S + T \\ S &\Rightarrow T \\ T &\Rightarrow T \times F \\ T &\Rightarrow F \\ F &\Rightarrow (S) \\ F &\Rightarrow a \\ \end{align}$$

і для ланцюжка $\omega = a \times (a + a)$ побудуємо лівосторонній аналіз $\pi$:

Виведення має вигляд:

$$\begin{multline*} S \Rightarrow T \Rightarrow T \times F \Rightarrow F \times F \Rightarrow a \times F \Rightarrow a \times (S) \Rightarrow a \times (S + T) \Rightarrow \\ \Rightarrow a \times (T + T) \Rightarrow a \times (F + T) \Rightarrow a \times (a + T) \Rightarrow a \times (a + F) \Rightarrow a \times (a + a). \end{multline*}$$

З наведеного вище виводу ланцюжка $\omega \in L(G)$ лівосторонній аналіз $\pi$ буде: $\pi = (2, 3, 4, 6, 5, 1, 2, 4, 6, 4, 6)$, а синтаксичне дерево виводу $\omega = a \times (a + a)$ наступне:

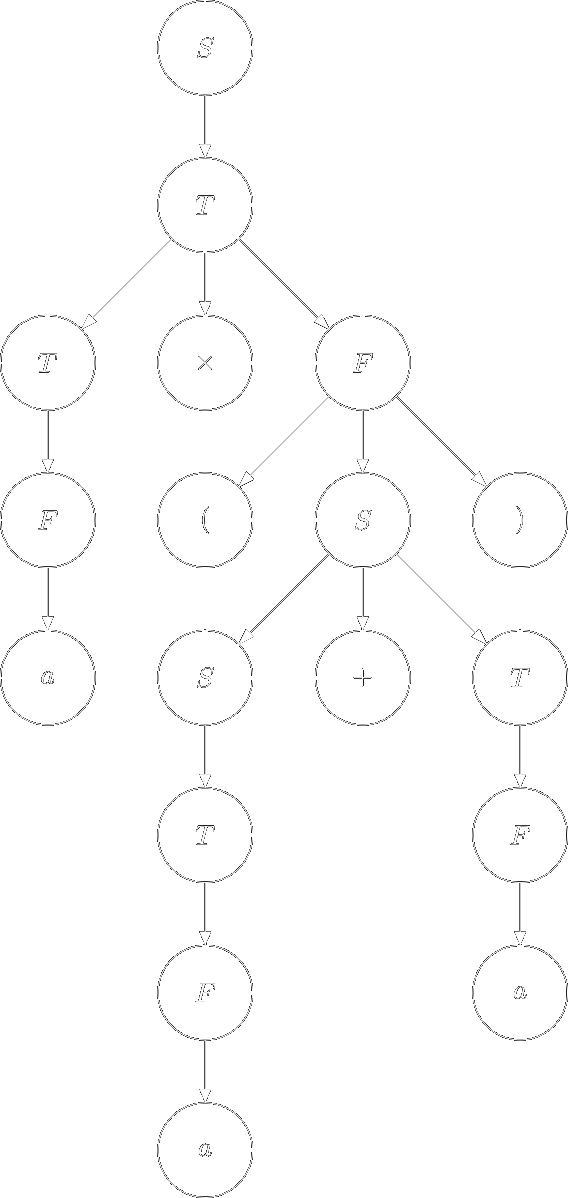
Синтез дерева за аналізом

Нехай $\pi$ — лівосторонній аналіз ланцюжка $\omega \in L(G)$. Знаючи $\pi$ досить легко побудувати (відтворити) синтаксичне дерево. Відтворення (синтез) синтаксичного дерева можна виконати, скориставшись однією з стратегій синтаксичного аналізу:

• стратегія “зверху донизу”;

• стратегія “знизу догори”.

Стратегія синтаксичного аналізу “зверху донизу” — це побудова синтаксичного дерева крок за кроком починаючи від кореня до крони.

Алгоритм [синтезу синтаксичного дерева на основі лівостороннього аналізу $\pi$ ланцюжка $\omega \in L(G)$].

1. Побудуємо корінь дерева та позначимо його аксіомою $S$. Тоді, якщо $\pi = (p_1, p_2, \ldots, p_m)$, то

2. Побудуємо дерево висоти один, взявши зі схеми $P$ правило з номером $p_1$ виду $S \Rightarrow \alpha_1 \alpha_2 \ldots \alpha_p$:

   

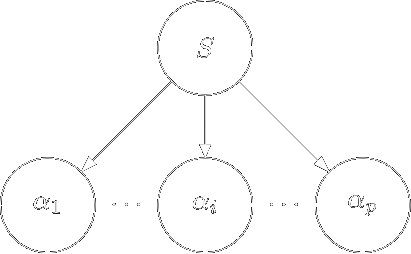
3. На кроні дерева, отриманого на попередньому кроку, візьмемо перший зліва направо нетермінал (нехай це буде нетермінал $\alpha_i$) та правило з номером $p_j$ вигляду: $\alpha_i \Rightarrow \beta_1 \beta_2 \ldots \beta_l$ та побудуємо нове дерево:

   

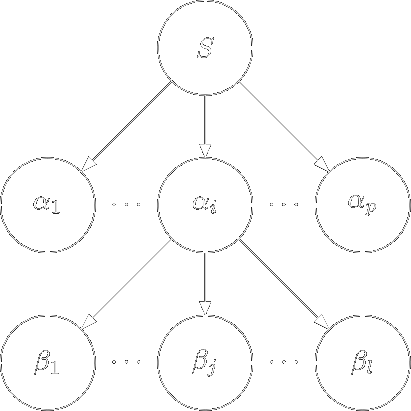
   Даний пункт виконувати доти, доки не переглянемо всі елементи з $\pi$.

Проблеми стратегії “зверху донизу”

Сформулюємо декілька проблему для стратегії аналізу “зверху донизу”:

У загальному випадку у класі КС-граматик існує проблема неоднозначності (недетермінізму) виводу $\omega \in L(G)$. Як приклад можемо розглянути граматику з “циклами”. Це така граматика, у якої в схемі $P$ існує така послідовність правил за участю нетермінала $A_i$, що: $A_i \Rightarrow A_j$ і $A_j \Rightarrow A_i$, де $A_j$ — будь-який нетермінал граматики $G$.

Як наслідок, граматики з ліворекурсивним нетерміналом для стратегії аналізу “зверху донизу” недопустимі.

Зауважимо, що існують підкласи класу КС-граматик, які природно забезпечують стратегію аналізу “зверху донизу”. Один з таких підкласів — це $LL(k)$-граматики, які забезпечують синтаксичний аналіз ланцюжка $\omega \in L(G)$ за час $O(n)$, де $n = \vert \omega \vert$, та при цьому аналіз є однозначним.

Контрольні запитання

1. Які граматики називаються однозначними?

2. Які дві стратегії виведення ви знаєте?

3. Що таке синтаксичне дерево виведення?

4. Що таке лівосторонній аналіз ланцюжка?

5. Що таке синтез дерева за аналізом?

6. Які дві стратегії синтезу дерева за аналізом ви знаєте?

7. Що таке граматика з циклами і які проблеми вона створює для стратегії “згори донизу”?

8. Який підклас КС-граматик забезпечує стратегію аналізу “зверху донизу”?

(традиційні відповіді можна переглянути у коментарях у вихідному коді цієї сторінки)

Назад до лекцій

Назад на головну