Зміст:
Скінченно-автоматні мови
Ознайомившись з деякими результатами теорії скінчених автоматів, спробуємо з’ясувати, які мови (множини слів) є скінчено-автоматними.
Базові мови
Твердження: Скінчено автоматними є наступні множини:
-
порожня словарна множина — \(\varnothing\);
-
словарна множина, що складається з одного \(\varepsilon\)-слова — \(\{\varepsilon\}\);
-
множина \(\{a\}\), \(a \in \Sigma\).
Доведення: в кожному випадку нам доведеться конструктивно побудувати відповідний скінчений автомат:
-
Довільний скінчений автомат з пустою множиною заключних станів (а мінімальний — з пустою множиною станів) допускає \(\varnothing\);
-
Розглянемо автомат \(M = \left\langle \{q_0\}, \Sigma, q_0, \delta, \{q_0\}\right\rangle\), у якому \(\delta\) не визначено ні для яких \(a \in \Sigma\). Тоді \(L(M) = \{\varepsilon\}\).
-
Розглянемо автомат \(M = \left\langle \{q_0, q_1\}, \Sigma, q_0, \delta, \{q_1\}\right\rangle\), у якому функція \(\delta\) визначена лише для пари \((q_0, a)\), а саме: \(\delta(q_0, a) = \{q_1\}\). Тоді \(L(M) = \{a\}\).
Операції над мовами
Твердження: Якщо \(M_1 = \left\langle Q_1, \Sigma, q_0^1, \delta_1, F_1 \right\rangle\) та \(M_2 = \left\langle Q_2, \Sigma, q_0^2, \delta_2, F_2\right\rangle\), що визначають відповідно мови \(L(M_1)\) та \(L(M_2)\), то скінченно-автоматними мовами будуть:
-
\(L(M_1) \cup L(M_2) = \left\{w \mid q \in L(M_1) \text{ or } q \in L(M_2)\right\}\);
-
\(L(M_1) \cdot L(M_2) = \left\{w = xy \mid x \in L(M_1), y \in L(M_2) \right\}\);
-
\(L(M_1)^\star = \{\varepsilon\} \cup L(M_1) \cup L(M_1)^2 \cup L(M_1)^3 \cup \ldots\).
Доведення: в кожному випадку нам доведеться конструктивно побудувати відповідний скінчений автомат:
-
Побудуємо автомат \(M = \left\langle Q, \Sigma, q_0, \delta, F \right\rangle\) такий, що \(L(M) = L(M_1) \cup L(M_2)\):
-
\(Q = Q_1 \cup Q_2 \cup \{q_0\}\), де \(q_0\) — новий стан \((q_0 \notin Q_1 \cup Q_2)\);
-
Функцію \(\delta\) визначимо таким чином:
\[\delta(q, a) = \begin{cases} \delta_1(q, a), & q \in Q_1, \\ \delta_2(q, a), & q \in Q_2, \\ \delta_1(q_0^1, a) \cup \delta_2(q_0^2, a), & q = q_0. \end{cases}\] -
Множина заключних станів:
\[F = \begin{cases} F_1 \cup F_2, & \text{if } \varepsilon \notin L_1 \cup L_2, \\ F_1 \cup F_2 \cup \{q_0\}, & \text{otherwise}. \end{cases}\]
Побудований таким чином автомат взагалі кажучи недетермінований.
Індукцією по \(i\) показуємо, що \((q_0, w) \models^i (q,\varepsilon)\) тоді і тільки тоді, коли \((q_0^1,w) \models^i (q,\varepsilon), q \in F_1\) або \((q_0^2,w) \models^i (q,\varepsilon), q \in F_2\).
-
-
Побудуємо автомат \(M = \left\langle Q, \Sigma, q_0, \delta, F \right\rangle\) такий, що \(L(M) = L(M_1) \cdot L(M_2)\):
-
\(Q = Q_1 \cup Q_2\);
-
\(q_0 = q_0^1\);
-
Функцію \(\delta\) визначимо таким чином:
\[\delta(q, a) = \begin{cases} \delta_1(q, a), & q \in Q_1 \setminus F_1, \\ \delta_2(q, a), & q \in Q_2, \\ \delta_1(q, a) \cup \delta_2(q_0^2,a), & q \in F_1. \end{cases}\] -
Множина заключних станів:
\[F = \begin{cases} F_2, & \text{if } \varepsilon \notin L_2, \\ F_1 \cup F_2, & \text{otherwise}. \end{cases}\]
-
-
Побудуємо автомат \(M = \left\langle Q, \Sigma, q_0, \delta, F \right\rangle\) такий, що \(L(M) = L(M_1)^\star\):
-
\(Q = Q_1 \cup \{q_0\}\), де \(q_0\) — новий стан \((q_0 \notin Q_1)\);
-
Функцію \(\delta\) визначимо таким чином:
\[\delta (q, a) = \begin{cases} \delta_1(q, a), & q \in Q_1 \setminus F_1, \\ \delta_1(q_0^1, a), & q = q_0, \\ \delta_1(q, a) \cup \delta_1(q_0^1, a), & q \in F_1. \end{cases}\] -
Множина заключних станів \(F = F_1 \cup \{q_0\}\).
-
Скінченні автомати та праволінійні граматики
Породжуюча граматика \(G\) — це четвірка
\[G = \left\langle N, \Sigma, P, S \right\rangle,\]де:
-
\(N\) — скінченна множина — допоміжний алфавіт (нетермінали);
-
\(\Sigma\) — скінченна множина — основний алфавіт (термінали);
-
\(P\) — скінченна множина правил вигляду
\[\alpha \mapsto \beta, \quad \alpha \in \left(N \cup \Sigma\right)^\star \times N \times \left(N \cup \Sigma\right)^\star, \quad \beta \in \left(N \cup \Sigma\right).\] -
\(S\) — виділений нетермінал (аксіома).
Класифікація граматик Хомського
В залежності від структури правил граматики діляться на чотири типи:
-
Тип 0: граматики загального вигляду, коли правила не мають обмежень, тобто
\[\alpha \mapsto \beta, \quad \alpha \in \left(N \cup \Sigma\right)^\star \times N \times \left(N \cup \Sigma\right)^\star, \quad \beta \in \left(N \cup \Sigma\right).\] -
Тип 1: граматики, що не укорочуються, коли обмеження на правила мінімальні, а саме:
\[\alpha \mapsto \beta, \quad \alpha \in \left(N \cup \Sigma\right)^\star \times N \times \left(N \cup \Sigma\right)^\star, \quad \beta \in \left(N \cup \Sigma\right), \quad \vert \alpha\vert \le \vert \beta\vert .\] -
Тип 2: контекстно-вільні граматики, коли правила в схемі \(P\) мають вигляд:
\[A_i \mapsto \beta, \quad A_i \in N, \quad \beta \in \left(N \cup \Sigma\right)^\star.\] -
Тип 3: скінченно-автоматні граматики, коли правила в схемі \(P\) мають вигляд:
\[A_i \mapsto w A_j, \quad A_i \mapsto w, \quad Ai \mapsto A_j w,\]де \(A_i, A_j \in N\), \(w \in \Sigma^\star\).
В класі скінченно-автоматних граматик виділимо так звані праволінійні граматики — це граматики, які в схемі Р мають правила вигляду:
\[A_i \mapsto w A_j, \quad A_i \mapsto w,\]де \(A_i, A_j \in N\), \(w \in \Sigma^\star\).
Нескладно довести, що клас праволінійних граматик співпадає з класом граматик типу 3.
Мова породжена граматикою
Ланцюжок \(w_1\) безпосередньо виводиться з ланцюжка \(w\) (позначається \(w \Rightarrow w_1\)), якщо \(w = x \alpha y\), \(w_1 = x \beta y\) та в схемі \(P\) граматики \(G\) є правило виду \(\alpha \mapsto \beta\). Оскільки поняття “безпосередньо виводиться” розглядається на парах ланцюжків, то в подальшому символ \(\Rightarrow\) буде трактуватися як бінарне відношення.
Ланцюжок \(w_1\) виводиться з ланцюжка \(w\) (позначається \(w \Rightarrow^\star w_1\)), якщо існує скінчена послідовність виду \(w \Rightarrow w_1' \Rightarrow w_2' \Rightarrow \ldots \Rightarrow w_n' \Rightarrow w_1\). Або кажуть, що бінарне відношення \(\Rightarrow^\star\) — це рефлексивно-транзитивне замикання бінарного відношення \(\Rightarrow\).
Мова, яку породжує граматика \(G\) (позначається \(L(G)\)) — це множина термінальних ланцюжків:
\[L(G) = \left\{ w \mid S \Rightarrow^\star w, w \in \Sigma^\star \right\}.\]Праволінійна граматика \(\sim\) скінченний автомат
Теорема. Клас мов, що породжуються праволінійними граматиками, співпадає з класом мов, які розпізнаються скінченими автоматами.
Доведення. Спочатку покажемо, що для довільної праволінійної граматики \(G\) можна побудувати скінчений автомат \(M\), такий що \(L(M) = L(G)\).
Розглянемо правила праволінійної граматики. Вони бувають двох типів: \(A_i \mapsto w A_j\), і \(A_i \mapsto w\).
На основі правил граматики \(G\) побудуємо схему \(P_1\) нової граматики, яка буде еквівалентною початковій, а саме:
-
правила виду \(A_i \mapsto а_1 а_2 \ldots a_p A_j\) замінимо послідовністю правил
\[\begin{aligned} A_i &\mapsto a_1 B_1, \\ B_1 &\mapsto a_2 B_2, \\ &\ldots \\ B_{p - 1} &\mapsto a_p A_j. \end{aligned}\] -
правила виду \(A_i \mapsto а_1 а_2 \ldots a_p\) замінимо послідовністю правил
\[\begin{aligned} A_i &\mapsto a_1 B_1, \\ B_1 &\mapsto a_2 B_2, \\ &\ldots \\ B_{p - 1} &\mapsto a_p B_p, \\ B_p &\mapsto \varepsilon. \end{aligned}\]
де \(B_1, B_2, \ldots\) — це нові нетермінали граматики \(G_1\).
Очевидно, що граматика \(G_1\) буде еквівалентна граматиці \(G\).
Далі, на основі граматики \(G_1\) побудуємо скінчений автомат \(M\), таким чином:
-
як імена станів автомата візьмемо нетермінали граматики \(G_1\);
-
початковий стан автомата позначається аксіомою \(S\);
-
функція \(\delta\) визначається діаграмою переходів, яка будується на основі правил вигляду \(A_i \mapsto a_k A_j\):
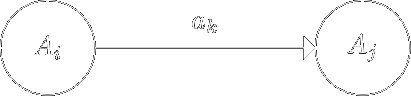
-
множина \(F\) заключних станів скінченого автомата визначається так: \(F = \{ A_i \mid A_i \mapsto \varepsilon \}\).
Індукцією по довжині вхідного слова покажемо, що якщо \(S \Rightarrow^{n + 1} w\), то \((q_0, w) \models^n (q, \varepsilon)\):
-
База: \(i = 0\): \(S \Rightarrow \varepsilon\), тоді \((q_0, \varepsilon) \models^0 (q_0, \varepsilon)\).
-
Перехід: нехай \(\vert w\vert = i + 1\), тобто \(w = a w_1\). Тоді \(S \Rightarrow a A_p \Rightarrow^i a w_1\) та \((q_0, a w_1) \models (q_i, w_1) \models^{i - 1} (q, \varepsilon)\), де \(q \in F\).
Доведення навпаки є очевидним.
Контрольні запитання
-
Які три базові скінченно-автоматні мови ви знаєте?
-
Доведіть, що мови з попереднього питання справді є скінченно-автоматними.
-
Які три операції над скінченно-автоматними мовами ви знаєте?
-
Доведіть, що результати операцій з попереднього питання справді є скінченно-автоматними.
-
Що таке породжуюча граматика?
-
Які чотири типи граматик за Хомським ви знаєте?
-
Що таке праволінійна граматика?
-
Дайте визначення безпосереднього виведення, виведення, породженої граматикою мови.
-
Доведіть, що скінченний автомат це майже праволінійна граматика.
(традиційні відповіді можна переглянути у коментарях у вихідному коді цієї сторінки)