Зміст:
Мінімізація детермінованих скінчених автоматів
В подальшому при програмуванні скінчених автоматів важливо мати справу з так званими “мінімальними автоматами”. Мінімальним для даного скінченого автомата називається еквівалентний йому автомат з мінімальною кількістю станів.
Нагадаємо, що два автомати називаються еквівалентними якщо вони розпізнають одну мову.
Те, що скінчені автомати можна мінімізувати покажемо на наступному прикладі:
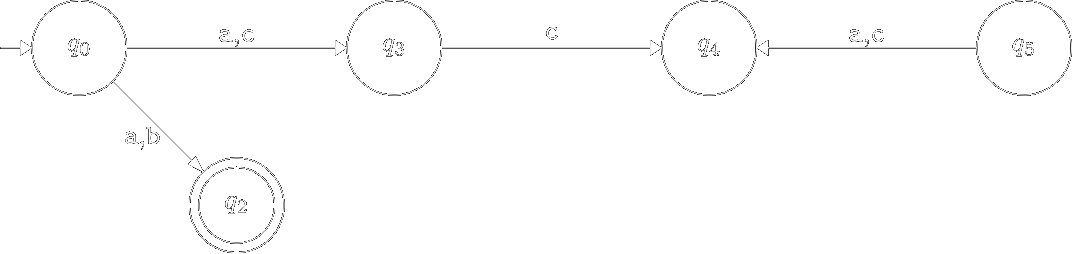
Навіть при поверхневому аналізі діаграми переходів наведеного скінченого автомата видно, що вершини \(q_3\), \(q_4\) та \(q_5\) є “зайвими”, тобто при їх вилученні новий автомат буде еквівалентний початковому. З наведеного вище прикладу видно, що для отриманого детермінованого скінченого автомата можна запропонувати еквівалентний йому автомат з меншою кількістю станів, тобто мінімізувати скінчений автомат. Очевидно що серед зайвих станів цього автомата є недосяжні та тупикові стани.
Недосяжні стани
Стан \(q\) скінченого автомата \(M\) називається недосяжним, якщо на діаграмі переходів скінченого автомата не існує шляху з \(q_0\) в \(q\).
Алгоритм [пошуку недосяжних станів]. Спочатку спробуємо побудувати множину досяжних станів. Якщо \(Q_m\) — множина досяжних станів скінченого автомата \(M\), то \(Q \setminus Q_m\) — множина недосяжних станів. Побудуємо послідовність множин \(Q_0, Q_1, Q_2, \ldots\) таким чином, що:
-
\(Q_0 = \{q_0\}\).
-
\(Q_i = Q_{i-1} \cup \left\{ q \mid \exists a \in \Sigma, q_j \in Q_{i - 1}: q \in \delta(q_j, a) \right\}\).
-
\(Q_m = Q_{m+1} = \ldots\).
Справді, очевидно, що кількість кроків скінчена, тому що послідовність \(Q_i\) монотонна \(\left(Q_0 \subseteq Q_1 \subseteq Q_2 \subseteq \ldots\right)\) та обмежена зверху: \(Q_m \subseteq Q\).
Тоді \(Q_m\) — множина досяжних станів скінченого автомата, а \(Q\setminus Q_m\) — множина недосяжних станів.
Вилучимо з діаграми переходів скінченого автомата \(M\) недосяжні вершини:
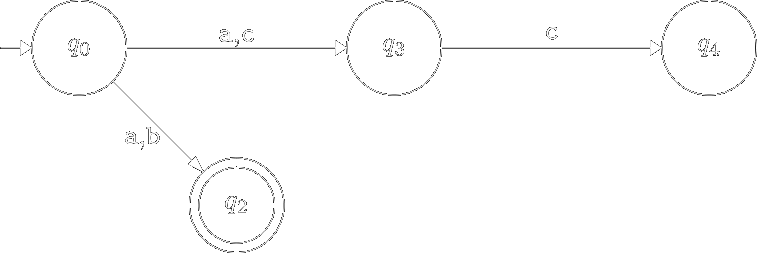
В новому автоматі функція \(\delta\) визначається лише для досяжних станів. Побудований нами скінчений автомат з меншою кількістю станів буде еквівалентний початковому.
Тупикові стани
Стан \(q\) скінченого автомата \(M\) називається тупиковим, якщо на діаграмі переходів скінченого автомата не існує шляху з \(q\) в \(F\).
Алгоритм [пошуку тупикових станів]. Спочатку спробуємо знайти нетупикові стани. Якщо \(S_m\) — множина нетупикових станів, то \(Q \setminus S_m\) — множина тупикових станів. Побудуємо послідовність множин \(S_0, S_1, S_2, \ldots\) таким чином, що:
-
\(S_0 = F\).
-
\(S_i = S_{i - 1} \cup \left\{ q \mid \exists a \in \Sigma: \delta(q, a) \cap S_{i - 1} \ne \varnothing \right\}\).
-
\(S_m = S_{m + 1} = \ldots\).
Очевидно, що кількість кроків скінчена, тому що послідовність \(S_i\) монотонна \(\left(S_0 \subseteq S_1 \subseteq S_2 \subseteq \ldots\right)\) та обмежена зверху — \(S_m \subseteq Q\).
Тоді \(S_m\) — множина нетупикових станів скінченого автомата, а \(Q \setminus S_m\) — множина тупикових станів.
Вилучимо з діаграми переходів скінченого автомата \(M\) тупикові вершини:
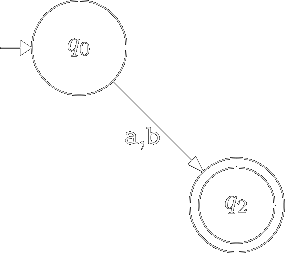
В новому автоматі функція \(\delta\) визначається лише для нетупикових станів.
Еквівалентні стани
Автомат, у котрого відсутні недосяжні та тупикові стани, піддається подальшій мінімізації шляхом “склеювання” еквівалентних станів. Продемонструємо це на конкретному прикладі:
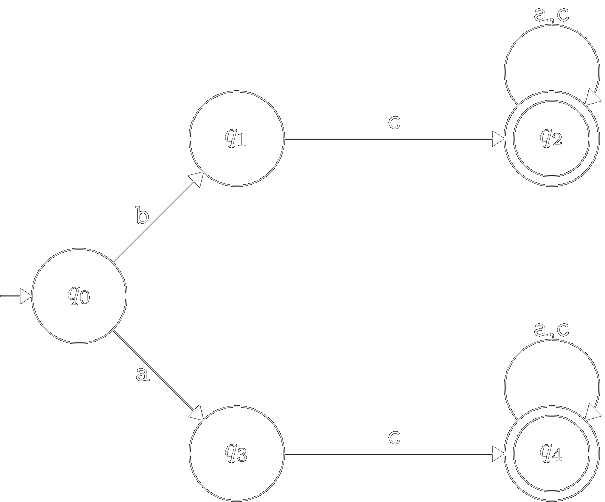
Очевидно, що для наведеного вище скінченого автомата можна побудувати еквівалентний йому скінчений автомат з меншою кількістю станів:
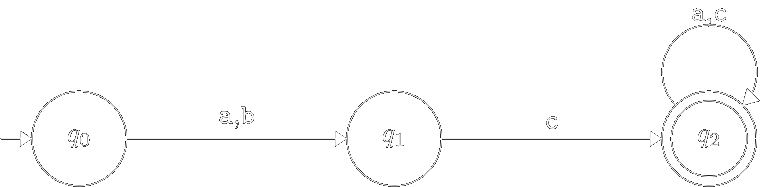
Ми досягли бажаного нам результату шляхом “склеювання” двох станів \(q_1 \equiv q_3\) та \(q_2 \equiv q_4\).
Два стани \(q_1\) та \(q_2\) скінченого автомата \(M\) називаються еквівалентними (позначається \(q_1 \equiv q_2\)), якщо множини слів, які розпізнає автомат, починаючи з \(q_1\) та \(q_2\), співпадають.
Нехай \(q_1\) та \(q_2\) — два різні стани скінченого автомата \(M\), а \(x \in \Sigma^\star\). Будемо говорити, що ланцюжок \(x\) розрізняє стани \(q_1\) та \(q_2\), якщо \((q_1,x) \models^\star (q_3, \varepsilon)\) та \((q_2,x) \models^\star (q_4, \varepsilon)\), причому рівно один зі станів \(q_3\) і \(q_4\) (не) належить множині заключних станів.
Стани \(q_1\) та \(q_2\) називаються \(k\)-нерозрізнені, якщо не існує ланцюжка \(x\) \((\left\vert x\right\vert \le k),\) що розрізняє стани \(q_1\) та \(q_2\).
Два стани \(q_1\) та \(q_2\) нерозрізнені, якщо вони \(k\)-нерозрізнені для довільного \(k\).
Теорема. Два стани \(q_1\) та \(q_2\) довільного скінченого автомата \(M\) з \(n\) станами нерозрізнені, якщо вони \((n - 2)\)-нерозрізнені.
Доведення: На першому кроці розіб’ємо множину станів скінченого автомата на дві підмножини: \(F\) та \(Q \setminus F\). На цій основі побудуємо відношення \(\equiv^0\): \(q_1 \equiv^0 q_2\), якщо обидва стани одночасно належать \(F\) або \(Q \setminus F\).
Побудуємо відношення \(\equiv^k\): \(q_1 \equiv^k q_2\), якщо \(q_1 \equiv^{k - 1} q_2\) та \(\delta(q_1,а) \equiv^{k - 1} \delta(q_2, а)\) для всіх \(а \in \Sigma\).
Очевидно, кожна побудована множина містить не більше \((n-1)\) елементи.
Таким чином, можна отримати не більше \((n-2)\) уточнення відношення \(\equiv^0\).
Відношення \(\equiv^{n - 2}\) визначає класи еквівалентних станів автомата \(M\).
Алгоритм
Алгоритм [побудови мінімального скінченого автомата].
-
Побудувати скінчений автомат без тупикових станів.
-
Побудувати скінчений автомат без недосяжних станів.
-
Знайти множини еквівалентних станів та побудувати найменший (мінімальний) автомат.
Контрольні запитання
-
Які автомати називаються еквівалентними?
-
Який стан автомату називається недосяжним?
-
Опишіть алгоритм пошуку недосяжних станів і доведіть його збіжність. Бонус: оцініть складність цього алгоритму за часом і пам’яттю.
-
Який стан автомату називається тупиковим?
-
Опишіть алгоритм пошуку тупикових станів і доведіть його збіжність. Бонус: оцініть складність цього алгоритму за часом і пам’яттю.
-
Які стани називаються еквівалентними?
-
Опишіть алгоритм пошуку еквівалентних станів і доведіть його збіжність. Бонус: оцініть складність цього алгоритму за часом і пам’яттю.
-
Опишіть алгоритм мінімізації детермінованого скінченного автомату. Бонус: виведіть з попередніх оцінок складність цього алгоритму за часом і пам’яттю.
(традиційні відповіді можна переглянути у коментарях у вихідному коді цієї сторінки)