Зміст:
Лексичний аналіз в мовних процесорах
Призначення: перетворення вхідного тексту програми з формату зовнішнього представлення в машинно-орієнтований формат — послідовність лексем.
Нагадаємо, що лексема — це ланцюжок літер елементарний об’єкт програми, що несе певний семантичний зміст. В подальшому кожну лексему будемо представляти як пару \(\langle\text{клас лексеми}, \text{ім'я лексеми}\rangle.\)
В більшості мов програмування для визначення класів лексем достатньо скінчених автоматів.
Скінчені автомати
Недетермінований скінчений автомат — це п’ятірка \(M = \left\langle Q, \Sigma, \delta, q_0, F \right\rangle,\) де
-
\(Q = \{q_0, q_1, \ldots, q_{n-1}\}\) — скінчена множина станів автомата;
-
\(\Sigma = \{a_1, a_2, \ldots, a_m\}\) — скінчена множина вхідних символів (вхідний алфавіт);
-
\(q_0 \in Q\) — початковий стан автомата;
-
\(\delta\) — відображення множини \(Q \times \Sigma\) в множину \(2^Q\). Відображення \(\delta\) як правило називають функцією переходів;
-
\(F \subset Q\) — множина заключних станів. Елементи з \(F\) називають заключними або фінальними станами.
Якщо \(M\) — скінчений автомат, то пара \((q, w) \in Q \times \Sigma^\star\) називається конфігурацією автомата \(M\). Оскільки скінчений автомат — це дискретний пристрій, він працює по тактам. Такт скінченого автомата \(M\) задається бінарним відношенням \(\models\), яке визначається на конфігураціях:
\[(q_1, a w) \models (q_2, w) \quad \text{if} \quad q_2 \in \delta(q_1, a), \quad \forall w \in \Sigma^\star.\]Мова яку розпізнає скінченний автомат
Скінчений автомат \(M\) розпізнає (допускає) ланцюжок \(w\), якщо
\[\exists q \in F: \quad (q_0, w) \models^\star (q, \varepsilon),\]де \(\models^\star\) — рефлексивно-транзитивне замикання бінарного відношення \(\models\).
Mова, яку допускає автомат \(M\) (розпізнає автомат \(M\))
\[L(M) = \{w \mid w \in \Sigma^\star, \exists q \in F: (q_0, w) \models^\star (q, \varepsilon)\}.\]Способи визначення функції переходів
На практиці, при визначенні скінченого автомата \(M\), використовують декілька способів визначення функції \(\delta\), наприклад:
-
це табличне визначення \(\delta\);
-
діаграма проходів скінченого автомата.
Табличне визначення функції \(\delta\) — це таблиця \(M(q_i, a_j),\) де \(a_j \in \Sigma, q_i \in Q,\) тобто
\[M(q_i, a_j) = \{ q_k \mid q_k \in \delta(q_i, a_j) \}.\]Діаграма переходів скінченого автомата \(M\) — це невпорядкований граф \(G(V, P)\), де \(V\) — множина вершин графа, а \(P\) — множина орієнтованих дуг, причому з вершини \(q_i\) у вершину \(q_j\) веде дуга позначена \(a_k\), коли \(q_j \in \delta(q_i, a_k)\). На діаграмі переходів скінченого автомата це позначається так:
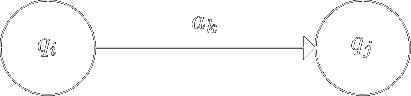
В подальшому, на діаграмі переходів скінченого автомата \(M\) елементи з множини заключних станів будемо позначити так:

Приклад. Побудуємо діаграму переходів скінченого автомата \(M\), який розпізнає множину цілочислових констант мови С.
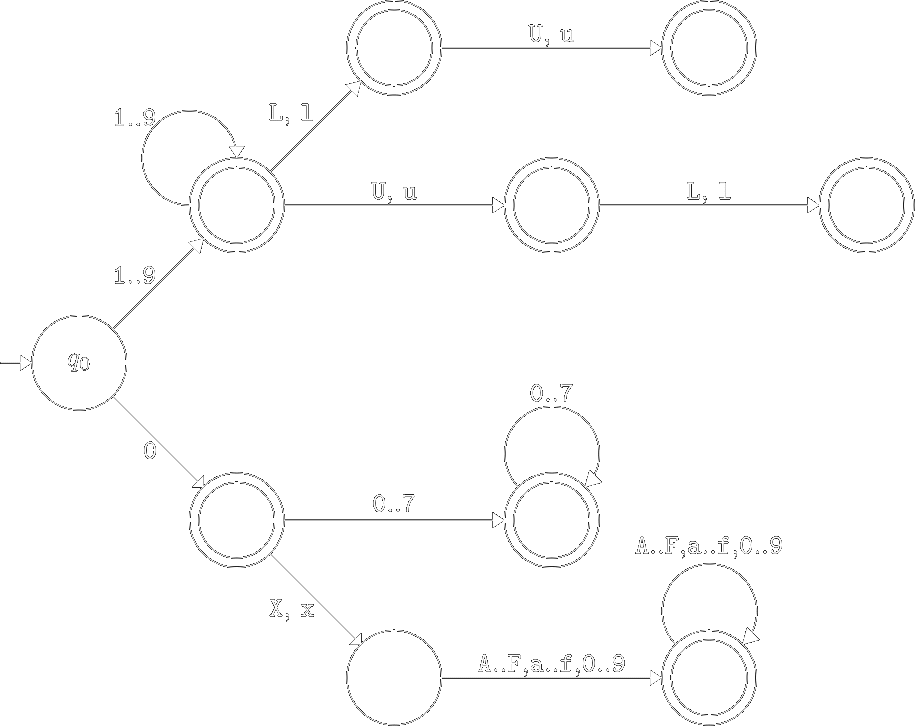
Зауваження. Цей автомат неповний, на два нижні праві вузли потрібно довісити “UL”-частину яка висить на вузлі “1..9”.
З побудованого прикладу видно, що приведений автомат не повністю визначений.
Детерміновані скінченні автомати
Скінчений автомат \(M\) називається детермінованим, якщо \(\delta(a_i, a_k)\) містить не більше одного стану для любого \(q_i \in Q\) та \(a_k \in \Sigma\).
Теорема. Для довільного недетермінованого скінченого автомата \(M\) можна побудувати еквівалентний йому детермінований скінчений автомат \(M'\), такий що \(L(M) = L(M').\)
Доведення: Нехай \(M\) — недетермінований скінчений автомат \(M = \langle Q, \Sigma, \delta, q_0, F\rangle.\)
Детермінований автомат \(M' = \langle Q', \Sigma, \delta', q_0', F\rangle\) побудуємо таким чином:
-
\(Q' = 2^Q\), тобто імена станів автомата \(M'\) — це підмножини множини \(Q\).
-
\(q_0' = \{q_0\} \in 2^Q = Q'\).
-
\(F'\) складається з усіх таких підмножин \(S \in 2^Q = Q'\), що \(S \cap F \ne \varnothing\).
-
\(\delta'(S, a) \models \{q \mid q \in \delta(q_i, a), q_i \in S\}\).
Доводимо індукцією по \(i\), що \((S, w) \models^i (S', \varepsilon)\), тоді і тільки тоді, коли \(S' = \{q \mid \exists q_i \in S: (q_i, w) \models^i (q, \varepsilon)\}\).
Зокрема, \((\{q_0\}, w) \models^\star (S', \varepsilon)\), для деякого \(S' \in F'\), тоді і тільки тоді, коли \(\exists q \in F: (q_0, w) \models^\star (q, \varepsilon)\).
Таким чином, \(L(M) = L(M')\).
Побудований нами автомат \(M\) має дві властивості: він детермінований та повністю визначений. До того ж кількість станів цього автомата \(2^n - 1\).
Контрольні запитання
-
У чому призначення лексичного аналізу?
-
Що таке недетермінований скінчений автомат?
-
Яку мову розпізнає скінченний автомат?
-
Які два способи визначення функції переходів ви знаєте?
-
Спробуйте “зламати” вищенаведений автомат для цілочислових констант мови C (зверніть увагу на зауваження).
-
Що таке детермінований скінчений автомат?
-
Сформулюйте і доведіть теорему про детермінізацію скінченного автомата.
-
Нехай функція переходів \(\delta\) не однозначна, але у той же час набуває не багато різних значень на одному наборі аргументів, наприклад не більше двох, тобто \(\vert M(q, a)\vert \le 2\) для довільних \(q \in Q\) і \(a \in \Sigma\). Чи можна тоді отримати кращу оцінку зверху на кількість станів еквівалентного детермінованого автомату ніж \(2^n - 1\)?
(традиційні відповіді можна переглянути у коментарях у вихідному коді цієї сторінки)