• 9. Чисельне інтегрування
  • 9.1. Постановка задачі чисельного інтегрування
  • 9.2. Квадратурні формули прямокутників
  • 9.3. Формула трапеції
  • 9.4. Квадратурна формула Сімпсона
  • 9.5. Принцип Рунге
  • 9.6. Квадратурні формули найвищого алгебраїчного степеня точності
  • 9.7. Частинні випадки квадратурної формули Гауса
  • 9.8. Обчислення невласних інтегралів
  • 9.9. Обчислення кратних інтегралів

9. Чисельне інтегрування

9.1. Постановка задачі чисельного інтегрування

Література:

• ЛМС, стор. 13–14;

• СГ, стор. 161–162.

Нехай потрібно знайти

\begin{equation} \label{eq:9.1.1} I(f) = \Int_a^b \rho(x) f(x) \diff x, \end{equation}

де $f$ — задана функція, $\rho(x) > 0$ — деякий ваговий множник. Ця задача часто вимагає чисельного вирішення, оскільки

• значна кількість інтегралів типу \eqref{eq:9.1.1} не можуть бути обчислені аналітично;

• інформація про функцію $f$ може бути задана у вигляді таблиці.

Нагадаємо, що за означенням

\begin{equation} I(f) = \Lim_{\Delta \to 0} \Sum_{i = 1}^n \rho(\xi_i) f(\xi_i) \Delta x_i, \end{equation}

де $\Delta x_i = x_i - x_{i-1}$, а $\{x_i\}_{i = 0}^n$ — розбиття проміжку $[a,b]$, $x_i \in [a,b]$, $\xi_i \in [x_{i-1}, x_i]$.

Означення: Тому візьмемо як наближення таку суму, яка називається квадратурною формулою:

\begin{equation} \label{eq:9.1.2} I_n(f) = \Sum_{k = 0}^n c_k f(x_k), \end{equation} де $x_k$ — вузли квадратурної формули, а $c_k$ — її вагові множники.

Задача полягає в тим, щоб вибрати $\{x_n, c_k\}^n_{k = 0}$, так щоб похибка була найменша:

\begin{equation} R_n(f) = I(f) - I_n(f) \to \Min \end{equation}

Означення: Квадратурну формулу \eqref{eq:9.1.2} називають квадратурною формулою замкненого типу, якщо $x_0 = a$ та $x_n = b$, і відкритого типу, якщо $x_0 > a$ та $x_n < b$.

Означення: Кажуть, що квадратурна формула \eqref{eq:9.1.2} має $m$-ий степінь алгебраїчної точності, якщо

\begin{equation} \forall f \in \pi_m: \quad R_n(f) = 0, \end{equation}

де $\pi_m$ — множина поліномів $m$-го степеня, і

\begin{equation} \exists P_{m + 1}(x) \in \pi_{m + 1}: \quad R_n(P_{m + 1}) \ne 0. \end{equation}

Цю умову можна замінити умовою

\begin{equation} R_n(x^\alpha) = 0, \quad \alpha = \overline{0, m}, \quad R_n(x^{m + 1}) \ne 0, \end{equation}

вона більш зручна для перевірки.

Розглянемо деякі підходи до побудови квадратурних формул:

1. Інтерполяційний. Він приводить до квадратурних формул інтерполяційного типу. В інтегралі \eqref{eq:9.1.1} покладають $f(x) \approx L_n(x)$ по деяких вузлах $\{x_k\}^n_{k = 0}$ (вузли фіксовані). Тоді:

   \begin{equation} \begin{aligned} I_n(f) &\approx I(L_n(x)) = \newline &= \Int_a^b \rho(x) \Sum_{k = 0}^m \frac{f(x_k) \omega_n(x)}{(x - x_k) \omega_n’(x)} \diff x = \newline &= \Sum_{k = 0}^n f(x_k) \Int_a^b \rho(x) \frac{\omega_n(x)}{(x - x_k) \omega_n’(x_k)} \diff x. \end{aligned} \end{equation}

   Отже вузлами цієї квадратурної формули є вузли інтерполяційного багаточлена, а вагові множники

   \begin{equation} c_j = \Int_a^b \rho(x) \frac{\omega_n(x)}{(x - x_k) \omega_n’(x_k)} \diff x \end{equation}

2. Найвищого алгебраїчного степеня точності. Вибираємо одночасно $x_k$ і $c_k$ з умови $R_n(x) = 0$, $\alpha = \overline{0, m}$, щоб $m$ було максимальним. Отримуємо систему нелінійних алгебраїчних рівнянь, розв’язавши яку отримуємо квадратурні формули найвищого алгебраїчного степеня точності.

3. Складені квадратурні формули. Проміжок $[a,b]$ розбиваємо на підпроміжки (наприклад однокової довжини), а потім на кожному проміжку використовуємо, з невеликим степенем, формули з пункту 1 або 2. Наприклад, для формул інтерполяційного типу:

   \begin{equation} \begin{aligned} I(f) &= \Sum_{i = 1}^N \Int_{x_{i - 1}}^{x_i} \rho(x) f(x) \diff x \approx \newline &\approx \Sum_{i = 1}^N \Sum_{k = 0}^n c_k^i f(x_k^i) = I_h(f). \end{aligned} \end{equation}

   Означення: Кажуть, що квадратурна формула складеного типу $I_h$ має порядок (степінь) точності $p$ по кроку $h$, якщо $R_h(f) = I(f) - I_h(f) = O(h^p)$.

4. Квадратурні формули оптимальні на класі функцій. Вибираємо $\{x_k, c_k\}$ так, щоб досягався

   \begin{equation} \Inf_{{x_k, c_k}} \Sup_{f \in F} R_n(f). \end{equation}

   Це ми можемо робити, коли знаємо з яким класом функцій маємо справу.

Зауваження 1 (про квадратурні формули інтерполяційного типу): При підвищенні степеня інтерполяції погіршується якість наближення функції внаслідок розбіжності процесу інтерполяції:

\begin{equation} | f - L_n|\void_C \not \xrightarrow[n \to \infty]{} 0. \end{equation}

Але

\begin{equation} R_n \xrightarrow[n \to \infty]{} 0. \end{equation} наприклад, для $f \in C([a,b])$.

І все ж таки розбіжність процесу інтерполювання дає взнаки:

\begin{equation} \Max_k |c_k| \xrightarrow[n \to \infty]{} \infty. \end{equation}

і це приводить до поганих наслідків чисельного інтегрування. Дійсно, розглянемо випадок, коли функція задана неточними значеннями:

\begin{equation} \tilde f(x_k) = f(x_k) + \delta_k, \quad |\delta_k| < \delta. \end{equation}

Тоді

\begin{equation} \delta I_n(f) = I_n (\tilde f) - I_n(f) = \Sum_{k = 0}^n c_k \delta_k. \end{equation}

Якщо всі $c_k > 0$, то

\begin{equation} |\delta I| = \Sum_{k = 0}^n c_k |\delta_k| \le \delta \Sum_{k = 0}^n c_k = \delta (b - a). \end{equation}

При $\rho \equiv 1$, якщо підставити $f \equiv 1$, то отримаємо

\begin{equation} b - a = \Int_a^b \diff x = \Sum_{k = 0}^n c_k. \end{equation}

При $\rho \ne 1$:

\begin{equation} \Sum_{k = 0}^n c_k = \Int_a^b \rho(x) \diff x, \end{equation}

бо хоча б нульовий степінь точності будь-яка квадратурна формула повинна мати.

Нагадаємо, що

\begin{equation} \Max_k |c_k| \xrightarrow[n \to \infty]{} \infty, \end{equation}

а оскільки $\Sum c_k > 0$, то $\exists c_k > 0$ і $\exists c_k < 0$, тому з ростом $n$ зростає $\vert c_k \vert$, а відповідно і вплив похибки на результат. Тому не можна використовувати великі степені і використовують складені квадратурні формули.

Зауваження 2: Ясно, що квадратурні формули інтерполяційного типу мають алгебраїчний степінь точності принаймні $m = n$, бо ми заміняємо $f \mapsto L_n$, а якщо $f \in \pi_n$, то $f \equiv L_n$. Але виявляється, що для парних $n$ та симетричному розташуванні вузлів інтегрування, $m = n + 1$, тобто алгебраїчний степінь точності на одиницю вищий степеня інтерполяції.

9.2. Квадратурні формули прямокутників

Література:

• СГ, стор. 162–163.

Припустимо, що $\rho \equiv 1$. Тоді можна побудувати такі квадратурні формули інтерполяційного типу при $n = 0$:

1. лівих прямокутників: $x_0 = a$: $I_0^L = (b - a) \cdot f(a)$;

2. правих прямокутників: $I_0^R = (b - a) \cdot f(b)$, $x_0 = b$;

3. середніх прямокутників:

   \begin{equation} \label{eq:9.2.1} I_0 = (b - a) \cdot f(x_0), \quad x_0 = \frac{a + b}{2} \end{equation}

Знайдемо тепер алгебраїчну степінь точності цих квадратурних формул. Для лівих прямокутників:

\begin{align} I_0^L(1) &= b - a = I(1), \newline I_0^L(x) &= (b - a) \cdot a \ne \nonumber \newline & \ne \frac{b^2 - a^2}{2} = \Int_a^b x \diff x = I(x), \end{align}

отже степінь точності $m = 0$. Така ж вона буде і для $I_0^R$. А для середніх прямокутників

\begin{align} I_0(x) &= (b - a) \cdot \frac{a + b}{2} = I(x), \newline I_0(x^2) &= (b - a) \cdot \left(\frac{a + b}{2}\right)^2 \ne \nonumber \newline &\ne \frac{b^3 - a^3}{3} = \Int_a^b x^2 \diff x = I(x^2), \end{align}

тому $m = 1$. Отож нею і будемо користуватися.

Оцінимо для неї похибку. Взагалі для формули інтерполяційного типу:

\begin{equation} \begin{aligned} R_n(f) &= I(f) - I_n(f) = \newline &= I(f) - I(L_n) = \newline &= I(f - L_n) = I(r_n) = \newline &= \Int_a^b r_n(x) \diff x, \end{aligned} \end{equation}

де $r_n(x)$ — залишковий член інтерполяції. Далі

\begin{equation} \begin{aligned} |R_n(f)| &\le (b - a) \cdot \Max_x |r_n(x)| \le \newline &\le (b - a) \cdot \frac{M_{n + 1}}{n + 1} \cdot \Max_x |\omega_n(x)|. \end{aligned} \end{equation}

Для $I_0$:

\begin{equation} \begin{aligned} |R_0(f)| &= \left| \Int_a^n r_0(x) \diff x \right| \le \newline &\le \Int_a^b |r_0(x)| \diff x \le \newline &\le \Int_a^b \frac{M_1}{1!} |x - x_0| \diff x = \newline &= M_1 \Int_a^b |x - x_0| \diff x \le \newline &\le M_1 \cdot \frac{b^2 - a^2}{4}. \end{aligned} \end{equation}

Але це погана оцінка, вона не використовує той факт, що квадратурна формула має степінь точності на одиницю вищу. Отримаємо кращу оцінку. Маємо при $f \in C^2([a,b])$:

\begin{equation} f(x) = f(x_0) + (x - x_0) \cdot f’(x_0) + \frac{(x - x_0)^2}{2} \cdot f’’(\xi), \end{equation}

де $x_0 \equiv \frac{a + b}{2}$, а $\xi \in [a, b]$. Тоді

\begin{equation} \begin{aligned} R_0(f) &= \Int_a^b f(x) \diff x \Int_a^b L_0(x) \diff x = \newline &= \Int_a^b (f(x) - f(x_0)) \diff x = \newline &= \Int_a^b \left((x - x_0) f’(x_0) + \frac{(x - x_0)^2}{2} f’’(\xi)\right) \diff x = \newline &= \Int_a^b \frac{(x - x_0)^2}{2} \cdot f’’(\xi) \diff x = \newline &= f’’(\eta) \Int_a^b \frac{(x - x_0)^2}{2} \diff x = \newline &= \frac{f’’(\eta)}{24} \cdot (b - a)^3. \end{aligned} \end{equation}

Таким чином

\begin{equation} \label{eq:9.2.2} |R_0(f)| \le \frac{M_2}{24} \cdot (b - a)^3 \end{equation}

Але тут у нас немає впливу на точність (величину похибки). Тому використовують формулу складеного типу. Якщо сітка рівномірна, то складена квадратурна формула прямокутників має вигляд

\begin{equation} \label{eq:9.2.3} I(f) = \Sum_{i = 1}^n \Int_{x_{i - 1}}^{x_i} f(x) \diff x \approx \Sum_{i = 1}^N h \cdot f ( \bar x_i) = I_h(f), \end{equation}

де $\bar x_i = x_{i - 1/2} = x_i - h/2$.

Оцінимо похибку цієї квадратурної формули:

\begin{equation} \begin{aligned} R_h(f) &= I(f) - I_h(f) = \newline &= \Sum_{i = 1}^N \Int_{x_{i - 1}}^{x_i} (f(x) - f(\bar x_i)) \diff x = \newline &= \Sum_{i = 1}^N f’’(\eta_i) \cdot \frac{h^3}{24}, \end{aligned} \end{equation}

\begin{equation} |R_h(f)| \le \frac{M_2}{24} n h^3 = \frac{M_2 h^2 (b - a)}{24}. \end{equation}

Тобто ця формула має степінь точності $p = 2$ по кроку $h$. (Не слід плутати з алгебраїчним степенем точності $m = 1$ для цієї формули).

Якщо $f(x) \in C^4([a,b])$, то

\begin{equation} \begin{aligned} f(x) - f(\bar x_i) &= f(\bar x_i) + (x - \bar x_i) f’(\bar x_i) + \newline & \quad + \frac{(x - \bar x_i)^2}{2} \cdot f’’(\bar x_i) + \newline & \quad + \frac{(x - \bar x_i)^3}{6} \cdot f’’’(\bar x_i) + \newline & \quad + \frac{(x - \bar x_i)^4}{24} \cdot f^{(4)}(\xi_i) - f(\bar x_i). \end{aligned} \end{equation}

При непарних степенях інтеграли пропадуть і тому:

\begin{equation} \begin{aligned} R_h(f) &= \Sum_{i = 1}^N \Int_{x_{i - 1}}^{x_i} \frac{(x - \bar x_i)^2}{2} \cdot f’’(\bar x_i) \diff x + \newline &\quad + \Sum_{i = 1}^n \Int_{x_{i - 1}}^{x_i} \frac{(x - \bar x_i)^4}{24} \cdot f^{(4)}(\xi_i) \diff x = \newline &= \frac{h^2}{24} \Sum_{i = 1}^N h \cdot f’’(\bar x_i) + \newline &\quad + \Sum_{i = 1}^N \frac{h^5 \cdot f^{(4)}(\eta_i)}{1920}. \end{aligned} \end{equation}

Оскільки

\begin{equation} \Sum_{i = 1}^N h \cdot f’’(\bar x_i) \end{equation}

це квадратурна формула середніх прямокутників для $f''(x)$ з похибкою $O(h^2)$, то

\begin{equation} R_h(f) = \frac{h^2}{24} \Int_a^b f^{\prime\prime}(x) \diff x + O(h^4) = O(h^4), \end{equation}

і

\begin{equation} R_h(f) = \overset{\circ} R_h (f) + \alpha(h), \end{equation}

де

\begin{equation} \label{eq:9.2.5} \overset{\circ} R_h (f) = \frac{h^2}{24} \Int_a^b f^{\prime\prime}(x) \diff x, \end{equation}

де $\alpha(h) = O(h^4)$.

Ця формула використовується для побудови програм, що автоматично вибирають крок інтегрування.

9.3. Формула трапеції

Література:

• СГ, стор. 164–165

Нехай $x_0 = a$, $x_1 = b$, $L_1(x) = f(x)$. Тоді отримаємо формулу:

\begin{equation} \label{eq:9.3.1} I_1(f) = \frac{b - a}{2} \cdot (f(a) + f(b)) \end{equation}

Формула має алгебраїчний степінь точності $m = 1$, оскільки $I(x^2) \ne I_1(x^2)$. Це формула замкненого типу. Залишковий член:

\begin{equation} \label{eq:9.3.2} \begin{aligned} R_1(f) &= \Int_a^b \frac{f’’(\xi)(x - a)(x - b)}{2} \diff x = \newline &= - \frac{(b - a)^3}{12} \cdot f’’(\xi). \end{aligned} \end{equation}

Оцінка залишкового члена:

\begin{equation} \label{eq:9.3.3} |R_1(f)| \le M_2 \cdot \frac{(b - a)^3}{12}. \end{equation}

З геометричної точки зору замінюється площа криволінійної трапецій площею звичайної трапеції.

Складена квадратурна формула трапецій:

\begin{equation} \label{eq:9.3.4} \begin{aligned} I_h(f) &= \Sum_{i = 1}^N \frac{h}{2} \cdot (f(x_{i - 1}) + f(x_i)) = \newline &= \frac{h}{2} \cdot f(a) + \Sum_{i = 1}^{N - 1} h \cdot f(x_i) + \frac{h}{2} \cdot f(b), \end{aligned} \end{equation}

де $x_i = a + i h$, $h = \frac{b - a}{N}$, $i = \overline{0, N}$ та

\begin{equation} \label{eq:9.3.5} |R_h(f)| \le M_2 \cdot \frac{b - a}{12} \cdot h^2, \quad f \in C^2([a,b]). \end{equation}

Якщо $f \in C^4([a,b])$, то

\begin{equation} R_h(f) = \overset{\circ} R_h(f) + \alpha(h), \end{equation}

де

\begin{equation} \label{eq:9.3.6} \overset{\circ} R_h(f) = - \frac{h^2}{12} \Int_a^b f’‘(x) \diff x, \end{equation}

а $\alpha(h) = O(h^4)$.

Задача 29: Використовуючи явний вигляд головних членів похибки складених квадратурних формул прямокутників та трапецій, побудувати лінійною комбінацією цих двох формул квадратурну формулу четвертого степеня точності за кроком $h$.

9.4. Квадратурна формула Сімпсона

Література:

• СГ, стор. 165–167.

Нехай $x_0 = a$, $x_1 = \frac{a + b}{2}$, $x_2 = b$. Замість $f$ використовуємо $L_2(x)$. Тоді отримаємо квадратурну формулу:

\begin{equation} \label{eq:9.4.1} I_2(f) = \frac{b - a}{6} \left( f(a) + 4 f \left( \frac{a + b}{2} \right) + f(b) \right). \end{equation}

Це квадратурна формула Сімпсона.

Задача 30: Довести, що алгебраїчна степінь точності квадратурної формули Сімпсона $m = 3$.

Задача 31: Довести, що для $f \in C^4([a,b])$ залишковий член квадратурної формули Сімпсона має місце представлення:

\begin{equation} \label{eq:9.4.2} \begin{aligned} & R_2(f) = \newline & \quad = \frac{1}{24} \Int_a^b (x - a) \left( x - \frac{a + b}{2} \right)^2 (x - b) f^{(4)}(\xi) \diff x = \newline & \quad = \frac{f^{(4)}(\xi)}{2880} \cdot (b - a)^5, \end{aligned} \end{equation}

та вірна оцінка:

\begin{equation} \label{eq:9.4.3} |R_2(f)| \le \frac{M_4}{2880} \cdot (b - a)^5. \end{equation}

Складена квадратурна формула Сімпсона має вигляд:

\begin{equation} \label{eq:9.4.4} \begin{aligned} I_h(f) &= \Sum_{i = 1}^N \frac{h}{6} \left( f(x_{i - 1}) + 4 f (x_{i - 1/2}) + f(x_i) \right) = \newline &= \frac{h}{6} ( f(x_0) + 4 f(x_{1/2}) + 2 f(x_1) + \ldots \newline &\quad \ldots + 2 f(x_{N - 1}) + 4 f(x_{N-1/2}) + f(x_N) ). \end{aligned} \end{equation}

Якщо $f \in C^4([a,b])$, то має місце оцінка:

\begin{equation} \label{eq:9.4.5} |R_h(f)| \le \frac{M_4}{2880} \cdot (b - a) \cdot h^4, \quad p = 4. \end{equation}

Якщо $f \in C^6([a,b])$, то

\begin{equation} R_h(f) = \overset{\circ} R_h(f) + \alpha(h), \end{equation}

де

\begin{equation} \label{eq:9.4.6} \overset{\circ} R_h(f) = \frac{h^4}{2880} \Int_a^b f^{(4)}(x) \diff x, \end{equation}

Задача 32: Побудувати інтерполяційну квадратурну формулу для $n = 3$, $x_0 = a$, $x_1 = \frac{3 a + b}{4}$, $x_2 = \frac{a + 3 b}{4}$, $x_3 = b$. Який алгебраїчний степінь точності вона має?

9.5. Принцип Рунге

Література:

• СГ, стор. 169–171.

Нехай задана деяка величина $I$ (сіткова функція, інтеграл, неперервна функція). Нехай $I_h \approx I$ та $I_n \to I$ при $h \to 0$. Нехай похибка послідовності $I_h$ представляється у вигляді:

\begin{equation} \label{eq:9.5.1} R_h = I - I_h = \overset{\circ} R_h + \alpha(h), \end{equation}

де $\overset{\circ}{R}_h = C \cdot h^m$ — головний член похибки, $C$ не залежить від $h$, $\alpha(h) = o(h^m)$. Обчислимо $I_{h/2}$. З \eqref{eq:9.5.1} випливає, що

\begin{align} I &= I_h + C h^m + \alpha(h), \newline I &= I_{h/2} + C \cdot \frac{h^m}{2^m} + \alpha(h). \end{align}

Звідси

\begin{equation} I_{h/2} - I_h = \frac{C h^m}{2^m} \cdot (2^m - 1) + \alpha(h). \end{equation}

З \eqref{eq:9.5.1}:

\begin{equation} \label{eq:9.5.2} \overset{\circ} R_{h/2} = \frac{C h^m}{2^m} = \frac{I_{h/2} - I_h}{2^m - 1}, \end{equation}

та

\begin{equation} \overset{\circ} R_h = \frac{2^m}{2^m - 1} \cdot (I_{h/2} - I_h). \end{equation}

Означення: Формула \eqref{eq:9.5.2} носить назву апостеріорної оцінки похибки обчислення $I$ за допомогою наближення $I_{h/2}$. (Апріорні оцінки це оцінки отримані до обчислення величини $I_h$, апостеріорні оцінки — під час її обчислення).

З формули \eqref{eq:9.5.2} впливає такий алгоритм обчислення інтегралу із заданою точністю $\varepsilon$:

• обчислюємо $I_h$, $I_{h/2}$, $\overset{\circ} R_{h/2}$;

• перевіряємо чи $\left\vert \overset{\circ} R_{h/2} \right\vert < \varepsilon$.

  • Якщо так, то $I \approx I_{h/2}$;

  • Якщо ж ні, то:

    • обчислюємо $I_{h/2}$, $I_{h/4}$, $\overset{\circ} R_{h/4}$;

    • перевіряємо $\left\vert \overset{\circ} R_{h/4} \right\vert < \varepsilon$ і т. д.

• Процес продовжуємо поки не буде виконана умова $\left\vert \overset{\circ} R_{h/2^k} \right\vert < \varepsilon$, $k = 1,2, \ldots$.

Зауваження: Ми даємо оцінку не похибки, а її головного члена з точністю $\alpha(h)$, тому такий метод може давати збої, якщо не виконана умова

\begin{equation} |\alpha(h)| \ll \left| \overset{\circ} R_{h/2^k} \right|. \end{equation}

За допомогою головного члена похибки можна отримати краще значення для $I$:

\begin{equation} \label{eq:9.5.3} \tilde I_{h/2} = I_{h/2}^{(1)} = I_{h/2} + \overset{\circ} R_{h/2} = \frac{2^m}{2^m - 1} \cdot I_{h/2} - \frac{1}{2^m - 1} \cdot I_h. \end{equation}

Це екстраполяційна формула Річардсона: $I_h - \tilde I_{h/2} = \alpha(h)$.

Для квадратурної формули трапецій $p = 2$ і

\begin{align} I - I_h &= C h^2 + O(h^4), \newline \overset{\circ} R_{h/2} &= \frac{I_{h/2} - I_h}{3}. \end{align}

Маємо

\begin{equation} R_h = - \frac{h^2}{12} \Int_a^b f’‘(x) \diff x + O(h^4) = O(h^2). \end{equation}

Отже, якщо застосовувати екстраполяційну формулу Річардсона, то

\begin{equation} \label{eq:9.5.4} \tilde I_{h/2} = \frac{4}{3} \cdot I_{h/2} - \frac{1}{3} \cdot I_h, \end{equation}

і $I_h - \tilde I_{h/2} = O(h^4)$.

Задача 33: Написати явний вигляд квадратурної формули, яка отримується екстраполяцією Річардсона з квадратурної формули трапецій.

Якщо невідомо $m$, то можна використати принцип Рунге для його знаходження. Для цього використаємо $I_h$, $I_{h/2}$, $I_{h/4}$:

\begin{align} I_{h/2} - I_h &= \frac{C h^m}{2^m} \cdot (2^m - 1) + \alpha(h), \newline I_{h/4} - I_{h/2} &= \frac{C h^m}{2^{2m}} \cdot (2^m - 1) + \alpha(h), \end{align}

З точністю $\alpha(h)$ маємо

\begin{equation} 2^m = \frac{I_{h/2} - I_h}{I_{h/4} - I_{h/2}}. \end{equation}

Звідки

\begin{equation} m = \log_2 \left( \frac{I_{h/2} - I_h}{I_{h/4} - I_{h/2}} \right). \end{equation}

Оцінка $\left\vert \overset{\circ}{R}_{h/4}\right\vert < \varepsilon$ — найбільш точна, тому $I \approx I_{h/4}$.

Покажемо чому формулу прямокутників рідко використовують з принципом Рунге. Нехай точки, в яких обчислюється значення функції позначаються: в $I_h$ — o, в $I_{h/2}$ — x.

Для формули трапецій використовуються такі точки:

I_h:   o _ _ _ o _ _ _ o _ _ _ o

I_h/2: o _ x _ o _ x _ o _ x _ o

Для формули прямокутників:

I_h:   _ _ o _ _ _ o _ _ _ o _ _

I_h/2: _ x _ x _ x _ x _ x _ x _

Як бачимо для формули трапецій необхідно підраховувати нові значення в $N$ точках, а для формули прямокутників в $2N$.

Для економного використання обчислених значень функції на сітці з кроком $h$ для формули трапецій запишемо:

\begin{equation} I_h = \frac{h}{2} \left( f(a) + 2 \Sum_{i = 1}^{N - 1} f(x_i) + f(b) \right), \end{equation}

\begin{equation} \begin{aligned} I_{h/2} &= \frac{h}{4} \left( f(a) + 2 \Sum_{i = 1}^{N - 1} f(x_i) + \right. \newline & \quad \left. + 2 \Sum_{i = 1}^{N - 1} f(x_{i-1/2}) + f(b) \right) = \newline &= \frac{1}{2} \cdot I_h + \frac{h}{2} \Sum_{i = 1}^{N - 1} f(x_{i - 1/2}). \end{aligned} \end{equation}

Отже, на одному кроці принципу Рунге кількість обчислень $Q_t = O(N)$, а для $Q_r = O(2N)$.

Цей принцип застосовується і для формули Сімпсона $m = 4$. Головна частина залишкового члена для цієї формули:

\begin{equation} \overset{\circ} R_{h/2} = \frac{I_{h/2} - I_h}{15}. \end{equation}

\begin{equation} \tilde I_{h/2} = \frac{16}{15} \cdot I_{h/2} - \frac{1}{15} \cdot I_h, \end{equation}

\begin{equation} I_h - \tilde I_{h/2} = O(h^6). \end{equation}

Розглянемо використання так званих адаптивних квадратурних формул, в яких змінний крок вибирається за принципом Рунге. Для цього запишемо формулу трапецій із змінним кроком:

\begin{equation} I_h(f) = \Sum_{i = 1}^N \frac{h_i}{2} \cdot (f(x_{i-1}) + f(x_i)), \end{equation}

де $h_i = x_i - x_{i-1}$.

Оцінимо похибку на кожному інтервалі:

\begin{equation} \begin{aligned} R_{h_i} &= I_i - I_{h_i} = \newline &= \Int_{x_{i - 1}}^{x_i} f(x) \diff x - \frac{h_i}{2} (f(x_{i-1}) + f(x_i)) = \newline &= - \frac{h_i^3}{6} \cdot f’‘(x_{i-1/2}) + O(h_i^5). \end{aligned} \end{equation}

Таким чином $p = 3$ і головний член похибки:

\begin{equation} \overset{\circ} R_{h/2} = \frac{I_{h_i/2} - I_{h_i}}{7}. \end{equation}

Умова припинення ділення навпіл проміжку $[x_{i-1}, x_i]$:

\begin{equation} \left| \overset{\circ} R_{h_i/2} \right| \le \frac{\varepsilon \cdot h_i}{b - a}. \end{equation}

Це забезпечує точність на всьому інтервалі

\begin{equation} \left| \overset{\circ} R_{h/2} \right| = \left| \Sum_{i=1}^N R_{h_i/2} \right| \le \Sum_{i=1}^N \frac{\varepsilon \cdot h_i}{b - a} = \varepsilon \cdot \frac{b - a}{b - a} = \varepsilon. \end{equation}

Ще одне застосування принципу Рунге — високоточне обчислення інтегралу від достатньо гладкої функції за допомогою таблиці Ромберга. Для побудови цієї таблиці обчислимо за допомоги складеної квадратурної формули трапецій із сталим кроком $h$ послідовність значень $I_h = I_h^{(0)}$, $I_{h/2} = I_{h/2}^{(0)}$, $I_{h/4} = I_{h/4}^{(0)}$, $I_{h/8} = I_{h/8}^{(0)}$, $\ldots$ які мають похибку $O(h^2)$. За допомогою екстраполяції Річардсона \eqref{eq:9.5.3} з коефіцієнтами лінійної комбінації $(4/3, -1/3)$ уточнимо ці значення (див. також формулу \eqref{eq:9.5.4}). Отримаємо $I_{h/2}^{(1)}$, $I_{h/4}^{(1)}$, $I_{h/8}^{(1)}$. Вони мають похибку $O(h^4)$. Знову використовуємо екстраполяцію Річардсона з коефіцієнтами лінійної комбінації $(16/15, -1/15)$. Отримаємо $I_{h/4}^{(2)}$, $I_{h/8}^{(2)}$, які мають точність $O(h^6)$ і т. д.

Означення: Отримані значення можна розмістити в такій таблиці Ромберга:

	$0$	$1$	$2$	$3$
$h$	$I_h^{(0)}$
$h/2$	$I_{h/2}^{(0)}$	$I_{h/2}^{(1)}$
$h/4$	$I_{h/4}^{(0)}$	$I_{h/4}^{(1)}$	$I_{h/4}^{(2)}$
$h/8$	$I_{h/8}^{(0)}$	$I_{h/8}^{(1)}$	$I_{h/8}^{(2)}$	$I_{h/8}^{(3)}$

Всі значення крім останнього $I_{h/8}^{(3)}$ можна оцінити за принципом Рунге (див. формулу \eqref{eq:9.5.2}). Використання формули $(72)$ для обчислення $I_{h/2^k}^{(0)}$ та лінійні комбінації \eqref{eq:9.5.2} дають простий та економічний алгоритм обчислення $I$. Початкове значення $h$ можна брати рівним $b - a$, або $\frac{b - a}{n}$, де $n$ ціле.

9.6. Квадратурні формули найвищого алгебраїчного степеня точності

Література:

• ЛМС, стор. 89–95;

• СГ, стор. 180–183;

• БЖК, стор. 113–115, стор. 102–108.

Розглянемо інтеграл:

\begin{equation} \label{eq:9.6.1} I(f) = \Int_a^b \rho(x) f(x) \diff x, \end{equation}

де

\begin{equation} \rho(x) > 0, \quad x \in [a, b], \quad \left| \Int_a^b \rho(x) x^i \diff x \right| < \infty \end{equation}

Розглянемо задачу побудови квадратурної формули:

\begin{equation} \label{eq:9.6.2} I_n(f) = \Sum_{k=1}^n c_k f(x_k), \end{equation}

яка при заданому $n$ була б точною для алгебраїчного багаточлена можливо більшого степеня.

Означення: Такі квадратурні формули існують, вони називаються квадратурні формули найвищого алгебраїчного степеня точності або формули Гауса (або Гауса-Крістофеля).

В \eqref{eq:9.6.2} невідомими є $c_k$, $x_k$, $k = \overline{1,n}$. Їх обирають з умови, що \eqref{eq:9.6.2} точна для будь-якого багаточлена степеня $p$, а це еквівалентно умові, щоб формула була точною для функції $f(x) = x^\alpha$, $\alpha = \overline{0,p}$. Звідси отримуємо умови:

\begin{equation} \label{eq:9.6.3} I_n(x^\alpha) = \Int_a^n \rho(x) x^\alpha \diff x = \Sum_{k=1}^n c_k x_k^\alpha, \quad \alpha = {0,p}. \end{equation}

Ми хочемо отримати формули для $m \to \max$. Щоб кількість рівнянь була рівною кількості невідомих нам потрібно, щоб $p + 1 = 2 n$.

Задача 34: Побудувати квадратурну формулу найвищого степеня точності (розв’язати систему рівнянь \eqref{eq:9.6.3} для $a = -1$, $b = 1$, $\rho(x) = 1$.

Теорема (Гаусса): Квадратурна формула \eqref{eq:9.6.2} буде точною для будь-якого багаточлена степеня $p = 2n - 1$, тобто $\forall f(x) \in \pi_{2n-1}$ тоді і тільки тоді, коли виконуються умови:

1. поліном $\omega(x) = (x - x_1) (x - x_2) \ldots (x - x_n)$ ортогональний з вагою $\rho(x)$ до будь-якого багаточлена степеня менше $n$, $Q_{n-1}$:

   \begin{equation} \label{eq:9.6.4} \Int_a^b \omega(x) Q_{n-1}(x) \rho(x) \diff x = 0; \end{equation}

2. формула \eqref{eq:9.6.2} є квадратурною формулою інтерполяційного типу, тобто коефіцієнти обчислюються за формулою:

   \begin{equation} \label{eq:9.6.5} c_k = \Int_a^b \rho(x) \frac{\omega(x)}{(x - x_k) \omega’(x_k)} \diff x. \end{equation}

Доведення:

1. Необхідність: Нехай формула \eqref{eq:9.6.2} точна для багаточлена степеня $p = 2n - 1$, тобто $I(f) = I_n(f)$, $\forall f(x) \in \pi_{2n - 1}$. Тоді

   \begin{equation} \begin{aligned} I(f) &= \Int_a^b \rho(x) \omega(x) Q_{n-1}(x) \diff x = \newline &= \Sum_{k=1}^n c_k \omega(x_k) Q_{n-1}(x_k) = 0. \end{aligned} \end{equation}

   Тобто виконується \eqref{eq:9.6.4}. Тепер покладемо

   \begin{equation} f(x) = \frac{\omega(x)}{(x - x_j) \omega’(x_j)} \in \pi_{n - 1} \subset \pi_{2n-1}. \end{equation}

   Отримаємо

   \begin{equation} \begin{aligned} \Int_a^b \rho(x) f(x) \diff x &= \Int_a^b \rho(x) \frac{\omega(x)}{(x - x_j) \omega’(x_j)} \diff x = \newline &= \Sum_{k=1}^n c_k \frac{\omega(x_k)}{(x_k - x_j) \omega’(x_j)} = \newline &= \Sum_{k=1}^n c_k \delta_{kj} = c_j. \end{aligned} \end{equation}

   тобто виконується і умова \eqref{eq:9.6.5}.

2. Достатність: Нехай виконується \eqref{eq:9.6.4} і \eqref{eq:9.6.5}. Подамо $\forall f(x) \in \pi_{2n-1}$ у вигляді

   \begin{equation} f(x) - \omega(x) Q_{n-1}(x) + R_{n-1}(x). \end{equation}

   Розглянемо

   \begin{equation} \begin{aligned} I(f) &= \Int_a^b \rho(x) f(x) \diff x = \newline &= \Int_a^b \rho(x) (\omega(x) Q_{n-1}(x) + R_{n-1}(x)) \diff x = \newline &= \Sum_{k=1}^n c_k \omega(x_k) Q_{n-1}(x_k) + \newline &\quad + \Sum_{k=1}^n c_k R_{n-1}(x_k). \end{aligned} \end{equation}

   Оскільки $R_{n-1}(x_k) = f(x_k) - \omega(x_k)Q_{n-1}(x_k) = f(x_k)$, то

   \begin{equation} I(f) = \Sum_{k=1}^n c_k f(x_k) = I_n(f). \end{equation}

   Тобто формула \eqref{eq:9.6.2} є точною для будь-якого багаточлена степеня $2n - 1$. $\square$

Отже, з точністю до сталого множника багаточлени $\omega(x)$ співпадають з багаточленами $n$-того степеня ортогональної системи багаточленів. Ця система ортогональна на проміжку $[a,b]$ з вагою $\rho(x)$.

Вивчимо деякі властивості квадратурних формул Гауса:

1. Покажемо, що $c_k$, $x_k$ визначаються однозначно.

   Представимо багаточлен $\omega(x)$ у вигляді

   \begin{equation} \omega(x) = a_0 + a_1 x + \ldots + a_{n-1} x^{n-1} + x^n. \end{equation}

   Умови ортогональності \eqref{eq:9.6.4} приймуть вигляд

   \begin{equation} \begin{aligned} & \Int_a^b \rho(x) \omega(x) x^\alpha \diff x = \newline & \quad = \Int_a^b \rho(x) (a_0 + \ldots + x^n) x^\alpha \diff x = 0, \end{aligned} \end{equation}

   де $\alpha = \overline{0,n-1}$, або

   \begin{equation} \begin{aligned} & \Int_a^b \rho(x) (a_0 + a_1 x+ \ldots + a_{n-1} x^{n-1}) x^\alpha \diff x = \newline & \quad = - \Int_a^b \rho(x) x^n x^\alpha \diff x. \end{aligned} \end{equation}

   Покажемо, що відповідна однорідна система рівнянь

   \begin{equation} \label{eq:9.6.6} \Int_a^b \rho(x) (a_0 + a_1 x+ \ldots + a_{n-1} x^{n-1}) x^\alpha \diff x = 0, \end{equation}

   де $\alpha = \overline{0,n-1}$, має єдиний розв’язок $a_0 = a_1 = \ldots = a_{n-1} = 0$.

   Помножимо систему \eqref{eq:9.6.6} на $a_\alpha$ і просумуємо по всіх $\alpha = \overline{0,n - 1}$:

   \begin{equation} \begin{aligned} & \Sum_{\alpha=0}^{n-1} a_\alpha \Int_a^b \rho(x) (a_0 + a_1 x + \ldots + a_{n-1} x^{n-1}) x^\alpha \diff x = \newline & \quad = \Int_a^b \rho(x) \Sum_{\alpha=0}^{n-1} \Sum_{j=0}^{n-1} a_j a_\alpha x^\alpha x^j \diff x = \newline & \quad = \Int_a^b \rho(x) \left( \Sum_{j=0}^{n-1} a_j x^j \right)^2 \diff x = 0. \end{aligned} \end{equation}

   Звідси і з умови $\rho(x) > 0$ випливає, що $a_0 = a_1 = \ldots = a_{n-1} = 0$. Тому і відповідна неоднорідна система має єдиний розв’язок. Отже існує єдиний багаточлен $\omega(x)$ степеня $n$, який ортогональний з вагою $\rho(x)$ до будь-якого багаточлена степеня $n - 1$.

2. Покажемо, що найвищий степінь точності формули Гаусса $p = 2 n - 1$. З теореми випливає, що $p \ge 2n - 1$. Покажемо, що існує багаточлен степеня $2n$, для якого формула не є точною. Для цього введемо функцію $f(x) = \omega^2(x) \in \pi_{2n}$. Маємо

   \begin{equation} I(f) = \Int_a^n \rho(x) \omega^2(x) \diff x > 0, \end{equation}

   але

   \begin{equation} I_n(f) = \Sum_{k=1}^n c_k \omega^2(x_k) = 0. \end{equation}

   Отже, $I(f) \ne I_n(f)$. Звідси $p \le 2n - 1$, тобто $p = 2n - 1$.

3. Коефіцієнти формул Гаусса додатні, тобто $c_k > 0$. Розглянемо багаточлени

   \begin{equation} \varphi_j = \left( \frac{\omega(x)}{(x-x_j)\omega’(x_j)} \right)^2, \end{equation}

   які мають степінь $2n - 2$ і властивості:

   \begin{equation} \varphi_i(x_k) = \delta_{ik}, \quad I(\varphi_j) = \Int_a^b \rho(x) \varphi_j(x) \diff x > 0. \end{equation}

   Оскільки для цих багаточленів справедлива теорема Гауса, то

   \begin{equation} \begin{aligned} I(\varphi_j) &= I_n(\varphi_j) = \newline &= \Sum_{k=1}^n c_k \varphi_j(x_k) = \newline &= \Sum_{k=1}^n c_k \left( \frac{\omega(x)}{(x-x_j)\omega’(x_j)} \right)^2 = \newline &= \Sum_{k=1}^n c_k \delta_{jk}^2 = c_j. \end{aligned} \end{equation}

   Звідси випливає, що $c_j > 0$, $j = \overline{1, n}$.

Теорема: Нехай вагова функція $\rho(x) > 0$, $x \in [a,b]$, $f(x) \in C^{2n}([a,b])$. Тоді існує точка $\xi \in [a,b]$ така, що

\begin{equation} R_n(f) = \frac{f^{(2n)}(\xi)}{(2n)!} \Int_a^b \rho(x) \omega^2(x) \diff x. \end{equation}

Доведення: Розглянемо інтерполяційний багаточлен Ерміта з двократними вузлами

\begin{equation} H_{2n-1}(x): f(x_i) = H_{2n-1}(x_i) \land f’(x_i) = H_{2n-1}’(x_i), \end{equation}

де $i = \overline{1,m}$. Для нього

\begin{equation} r_{2n-1}(x) = f(x) - H_{2n-1}(x) = \frac{f^{(2n)}(\xi)}{(2n)!} \cdot \omega^2(x). \end{equation}

Звідси

\begin{equation} \begin{aligned} R_{2n-1}(x) &= \Int_a^b \rho(x) r_{2n-1}(x) \diff x = \newline &= \frac{f^{(2n)}(\xi)}{(2n)!} \Int_a^b \rho(x) \omega^2(x) \diff x. \quad \square \end{aligned} \end{equation}

9.7. Частинні випадки квадратурної формули Гауса

Література:

• ЛМС, стор. 99.

1. Розглянемо відрізок $[-1,1]$ і ваговий множник $\rho(x) = 1$, тобто виведемо формули Гауса для обчислення інтегралу

   \begin{equation} \Int_{-1}^1 f(x) \diff x. \end{equation}

   Щоб знайти вузли квадратурна формули розглянемо багаточлени Лежандра:

   \begin{equation} (n + 1) L_{n+1}(x) = (2 n + 1) x L_n(x) - n L_{n-1}(x), \end{equation}

   де $L_0 = 1$, $L_1(x) = x$.

   Багаточлени Лежандра задовольняють умовам теореми $1$ (пункт $1$), тому $\omega(x) = L_n(x)$ і вузлами квадратурної формули є корені цього багаточлена. Вагові множники цієї формули обчислюються за формулою

   \begin{equation} c_k = \Int_{-1}^1 \frac{\omega(x)}{(x - x_k) \omega’(x_k)} \diff x, \end{equation}

   а залишковий член

   \begin{equation} R_n(f) = \frac{2^{2n+1}}{(2n+1)!(2n)!} \cdot \frac{(n!)^2}{(2n!)} \cdot f^{(2n)}(\xi). \end{equation}

   Приклад: Побудуємо квадратурну формулу \begin{equation} \Int_0^1 f(x) \diff x \approx \Sum_{k=1}^n c_k f(x_k). \end{equation} При \(n = 2\) потрібно знайти \(c_0\), \(c_1\), \(x_0\), \(x_1\).

   Розв’язок: Заміною $t = 2 x - 1$ переведемо $x \in [0,1]$ на проміжок $t \in [-1,1]$. Запишемо $L_2(t) = 3 t^2 / 2 - 1 / 2$. Звідси

   \begin{equation} \begin{aligned} L_2(x) &= \frac{3 (2 x - 1) - 1}{2} = \newline &= \frac{12 x^2 - 12 x + 2}{6} = \newline &= 6 x^2 - 6 x + 1 = 0. \end{aligned} \end{equation}

   Звідси $x_1 = \frac{3 - \sqrt{3}}{6}$, $x_2 = \frac{3 + \sqrt{3}}{6}$. За формулою \eqref{eq:9.6.5} знайдемо

   \begin{align} c_1 &= \Int_0^1 \frac{x - x_2}{x_1 - x_2} \diff x = \frac{1}{2}, \newline c_2 &= \Int_0^1 \frac{x - x_1}{x_2 - x_1} \diff x = \frac{1}{2}. \end{align}

   Тобто квадратурна формула має вигляд

   \begin{equation} \begin{aligned} & \Int_0^1 f(x) \diff x = \newline & \quad = \frac{1}{2} \left( f \left( \frac{3 - \sqrt{3}}{6} \right) + f \left( \frac{3 + \sqrt{3}}{6} \right) \right). \end{aligned} \end{equation}

2. Розглянемо відрізок $[-1, 1]$ і вагу $\rho(x) = 1 / \sqrt{1 - x^2}$, тобто виведемо формулу Гауса для обчислення інтегралу

   \begin{equation} I(f) = \Int_{-1}^1 \frac{f(x) \diff x}{\sqrt{1 - x^2}}. \end{equation}

   Багаточлени Чебишова задовольняють умовам теореми $1$ (п.$1$), тому

   \begin{equation} \omega(x) = \overline T_n (x) = \frac{\cos (n \arccos (x))}{2^{n - 1}}. \end{equation}

   Вузлами квадратурної формули є корені цього багаточлена Чебишова, тобто корені рівняння $\cos(n \arccos (x)) = 0$. Звідси

   \begin{equation} x_k = \cos \left( \frac{(2 k - 1) \pi}{2 n} \right), \quad k = \overline{1, n}. \end{equation}

   Відповідні коефіцієнти обчислюються за формулами

   \begin{equation} c_k = \Int_{-1}^1 \frac{\overline T_n(x) \diff x}{\sqrt{1 - x^2} T_n’(x) (x - x_k)} = \frac{\pi}{n}, \end{equation}

   для $k = \overline{1, n}$.

   Означення Отже, квадратурні формули найвищого степеня точності (ці формули називають формулами Ерміта) мають вигляд \begin{equation} \label{eq:9.7.1} I_n(f) = \frac{\pi}{n} \Sum_{k = 1}^n f(x_k), \end{equation} де \(x_k\) — корені багаточлена Чебишова.

   Залишковий член має вигляд

   \begin{equation} R_n(f) = \frac{\pi}{2^{2n - 1} (2n)!} \cdot f^{(2n)}(\xi). \end{equation}

3. Розглянемо проміжок $(-\infty, \infty)$ і вагу $\rho(x) = \exp\{-x^2\}$, тобто виведемо формулу Гауса для обчислення інтегралу

   \begin{equation} \Int_{-\infty}^\infty \exp\{-x^2\} f(x) \diff x. \end{equation}

   За теорією

   \begin{equation} \omega(x) = H_n(x) = (-1)^n e^{x^2} \frac{\diff^n}{\diff x^n} e^{-x^2}, \end{equation}

   де $H_n(x)$ — багаточлени Ерміта. Багаточлени Ерміта обчислюються також за рекурентними формулами

   \begin{equation} H_{n+1}(x) = 2 x H_n(x) - 2 n H_{n-1}(x), \end{equation}

   з початковими умовами $H_{-1} = 0$, $H_0 = 1$.

   Коефіцієнти квадратурної формули обчислюються за формулами

   \begin{equation} c_k = \frac{2^{n+1} n! \sqrt{\pi}}{(H_n’(x_k))^2} \end{equation}

   Залишковий член

   \begin{equation} R_n(f) = \frac{n! \sqrt{\pi}}{2^n (2n)!} \cdot f^{(2n)}(\xi). \end{equation}

   Наприклад: при \(n = 1\), \(H_1 (x) = 2x\). Корінь \(x_0 = 0\), \begin{equation} c_0 = \Int_{-\infty}^\infty \exp\{-x^2\} \diff x = \sqrt{\pi}. \end{equation} Квадратурна формула має вигляд: \begin{equation} I_1(x) = \sqrt{\pi} f(0). \end{equation}

4. Розглянемо відрізок $[0,\infty]$ і ваговий множник $\rho(x)= x^\alpha e^{-x}$, тобто виведемо формулу Гауса для обчислення інтегралу

   \begin{equation} \Int_0^\infty x^\alpha e^{-x} f(x) \diff x. \end{equation}

   За теорією

   \begin{equation} \omega(x) = L_n^\alpha (x) = (-1)^n x^{-\alpha} e^x \frac{\diff^n}{\diff x^n} (x^{\alpha + n} e^{-x}), \end{equation}

   де $L_n^\alpha(x)$ — багаточлени Лагера. Коефіцієнти обчислються за формулами

   \begin{equation} c_k = \frac{P(n + 1) P(n + \alpha + 1)}{x_k (L_n^\alpha(x_k))^2}. \end{equation}

   Залишковий член при $\alpha = 0$ рівний

   \begin{equation} R_n(f) = \frac{(n!)^2}{(2n)!} \cdot f^{(2n)}(\xi). \end{equation}

5. Інтегрування швидко осцилюючих функцій.

   Розглянемо інтеграл

   \begin{equation} I(f) = \Int_a^b f(x) e^{j \omega x} \diff x, \quad j^2 = -1. \end{equation}

   При великих $\omega$ застосування складених квадратурних формул інтерполяційного типу приводить до великої похибки і при малих кроках $h$. Розглянемо $e^{j \omega x}$ як ваговий коефіцієнт, тобто $\rho(x) = e^{j \omega x}$. Замінимо $[a,b]$ на $[-1,1]$:

   \begin{equation} x_i = \frac{a + b}{2} + \frac{b - a}{2} \cdot d_j, \end{equation}

   де $d_j \in [-1, 1]$, а $i = \overline{1,n}$.

   Зауваження: вузли можуть бути не рівновіддалені, якщо рівновіддалені, то \(d_i = -1 + 2 i / 2n\), \(i = \overline{1,n}\).

   Замінимо $f(x)$ на інтерполяційний багаточлен Лагранжа $L_{n-1}(x)$ з вузлами $x_i$ і отримаємо формулу

   \begin{equation} \label{eq:9.7.2} I_n(f) = \Int_a^b L_{n-1}(x) e^{j \omega x} \diff x, \end{equation}

   яка буде точною для всіх багаточленів не вище $n - 1$ степеня. Тобто, якщо в \eqref{eq:9.7.2} підставити багаточлен Лагранжа, то можна обчислити інтеграл і отримати квадратурну формулу

   \begin{equation} \begin{aligned} S_n^\omega(f) &= \frac{b - a}{2} \cdot \exp \left\{ j \omega \cdot \frac{a + b}{2} \right\} \cdot \newline & \quad \cdot \Sum_{i=1}^n D_i \left( \omega \cdot \frac{b - a}{2} \right) f(x_i), \end{aligned} \end{equation}

   де

   \begin{equation} D_i(p) \Int_{-1}^1 \left( \Prod_{\substack{k = 1 \\ k \ne i}}^n \frac{\xi - d_k}{d_i - d_k} \right) \exp \{j p \xi\} \diff \xi. \end{equation}

   При $n = 3$, $d_1 = -1$, $d_2 = 0$, $d_3 = 1$ це формула Філона. Можна брати і більше точок, наприклад, $n = 5$, $d_1 = -1$, $d_2 = -1/2$, $d_3 = 0$, $d_4 = 1/2$, $d_5 = 1$.

   Ці формули не потрібно застосовувати, коли немає швидко осцилюючого множника.

9.8. Обчислення невласних інтегралів

Література:

• БЖК, стор. 146–153

Розглянемо обчислення інтегралів з такими особливостями:

1. інтеграли другого роду, тобто

   \begin{equation} I = \Int_a^b F(x) \diff x, \quad F(x) \xrightarrow[x \to a \lor x \to b]{} \infty; \end{equation}

2. інтеграли першого роду

   \begin{equation} I = \Int_a^\infty F(x) \diff x. \end{equation}

Розглянемо спочатку інтеграли другого роду, тобто:

\begin{equation} I = \Int_a^b F(x) \diff x, \quad F(x) \xrightarrow[x \to a \lor x \to b]{} \infty. \end{equation}

1. Мультиплікативний спосіб. Представимо підінтегральну функцію у вигляді $F(x) = \rho(x) f(x)$, причому $\rho(x)$ — особлива, а $f(x)$ — гладка. Далі для обчислення інтегралу

   \begin{equation} I = \tilde I(f) = \Int_a^b \rho(x) f(x) \diff x \end{equation}

   використовуємо відповідні квадратурні формули Гаусса.

   Приклад 1: Потрібно обчислити інтеграл \begin{equation} I = \Int_{-1}^1 \frac{\diff x}{\sqrt{1 - x^4}}. \end{equation}

   Розв’язок: Точки $x = \pm 1$ є особливими.

   Представимо підінтегральну функцію у вигляді:

   \begin{equation} F(x) = \underset{\rho(x)}{\underbrace{\frac{1}{\sqrt{1 - x^2}}}} \cdot \underset{f(x)}{\underbrace{\frac{1}{\sqrt{1 + x^2}}}} \end{equation}

   отримаємо інтеграл вигляду

   \begin{equation} I = \Int_0^1 \frac{1}{\sqrt{1 + x^2}} \frac{\diff x}{\sqrt{1 - x^2}}, \end{equation}

   де $\rho(x) = 1 / \sqrt{1 - x^2}$.

   Далі використовуємо квадратурну формулу Ерміта \eqref{eq:9.7.1} з попереднього пункту і обчислюємо інтеграл.

   Приклад 2: Обчислити інтеграл

   \begin{equation} I = \Int_0^\pi \ln(\sin(x)) \diff x. \end{equation}

   Розв’язок: Особливі точки $x = 0$, $x = \pi$.

   Зведемо цю особливість до степеневої:

   \begin{equation} \rho(x) = \frac{1}{\sqrt{x (\pi - x)}}, \end{equation}

   тоді

   \begin{equation} f(x) = \sqrt{x (\pi - x)} \cdot \ln(\sin(x)) \xrightarrow[x \to 0, \pi]{} 0. \end{equation}

   Для знаходження інтегралу з таким $\rho(x)$ застосовуємо квадратурні формули Чебишова. Неприємності виникають, оскільки $f'(x) \xrightarrow[x \to 0,\pi]{} \infty$ (хоча квадратурні формули даватимуть наближене значення). Тому застосовують другий спосіб розв’язання проблеми:

2. Адитивний спосіб. Представимо підінтегральну функцію у вигляді $F(x) = f(x)+ \psi(x)$, причому $\psi(x)$ — особлива, $f(x)$ — гладка. Розбиваємо інтеграл на два: $I = I_1 + I_2$.

   1. $I_1 = \Int_a^b f(x) \diff x$ — обчислюють чисельно (наприклад, формули Сімпсона чи трапецій),

   2. $I_2 = \Int_a^b \psi(x) \diff x$ — пробують обчислити аналітично (можливо апроксимувати функцію $\psi(x)$, наприклад, рядом).

   Приклад 3: Обчислити інтеграл з прикладу $2$.

   \begin{align} I &= \Int_0^\pi \ln(\sin(x)) \diff x, \newline I &= 2 \Int_0^{\pi/2} \ln(\sin(x)) \diff x. \end{align}

   Представимо

   \begin{equation} \ln(\sin(x)) = \ln \left( \frac{\sin x}{x} \right) + \ln(x). \end{equation}

   Отримаємо два інтеграли:

   1. $I_1 = \Int_a^b \ln\left(\frac{\sin x}{x}\right) \diff x$ обчислюємо чисельно,

   2. $I_2 = \Int_0^{\pi/2} \ln(x) \diff x = \frac{\pi}{2} \left( \ln \left( \frac{\pi}{2} \right) - 1 \right)$.

Розглянемо тепер інтеграли першого роду

\begin{equation} I = \Int_a^\infty F(x) \diff x. \end{equation}

1. Заміни.

   • Нехай $a > 0$. Зробимо заміну $t = \frac{x - a}{x}$, $x = \frac{a}{1 - t}$. Тоді

     \begin{equation} I = a \Int_0^1 F \left( \frac{a}{1 - t} \right) \frac{\diff t}{(1 - t)^2}, \end{equation}

     а це інтеграл другого роду.

   • Якщо $a = 0$, то робимо заміну $t = e^{-x}$, $x = - \ln(t)$, тоді

     \begin{equation} I = \Int_0^1 F(-\ln(t)) \cdot \frac{\diff t}{t}. \end{equation}

     Знову отримуємо інтеграл другого роду.

   • Якщо $a < 0$ (не можна зробити заміну $t = \frac{x - a}{x}$, тому що виникає особливість в точці $x = 0$), розбиваємо інтеграл на два:

     \begin{equation} I = \Int_a^0 F(x) \diff x + \Int_0^\infty F(x) \diff x \end{equation}

     і обчислюємо за допомогою попередніх пунктів.

2. Мультиплікативний спосіб обчислення інтегралів першого роду ґрунтується на представлені підінтегральної функції у вигляді

   \begin{equation} F(x) = \rho(x) f(x), \end{equation}

   де, наприклад,

   \begin{equation} \rho(x) = x^\alpha \cdot e^{-x}, \quad x \in [0, \infty). \end{equation}

   Такий ваговий коефіцієнт відповідає багаточленам Лагера. При $x \in (-\infty, \infty)$, $\rho(x) = \exp\{-x^2\}$ приходимо до багаточленів Ерміта.

3. Обрізання границі. Ще один спосіб ґрунтується на обрізанні верхньої границі. Для цього інтеграл запишемо у вигляді

   \begin{equation} I = \Int_a^\infty F(x) \diff x = \Int_a^b F(x) \diff x + \Int_b^\infty F(x) \diff x. \end{equation}

   Верхня границя $b$ обчислюють з умови

   \begin{equation} \left| \Int_b^\infty F(x) \diff x \right| < \frac{\varepsilon}{2}, \end{equation}

   де $\varepsilon$ — задана точність. Для обчислення $\Int_a^b F(x) \diff x$ використовують квадратурні формули складеного типу.

9.9. Обчислення кратних інтегралів

Література:

• Волков, стор. 125–129;

• Калиткин, стор. 108–113, стор. 121–123.

Розглянемо інтеграл

\begin{equation} \label{eq:9.9.1} I = \Int_{a}^{b} \Int_{c}^{d} f(x,y) \diff x \diff y. \end{equation}

Цей інтеграл зводиться до повторного, якщо ввести

\begin{equation} \label{eq:9.9.2} F(x) = \Int_{c}^{d} f(x,y) \diff y. \end{equation}

Тоді

\begin{equation} \label{eq:9.9.3} I = \Int_a^b F(x) \diff x. \end{equation}

До однократних інтегралів можна застосувати квадратурну формулу середніх прямокутників. Тоді

\begin{equation} \begin{aligned} I &\approx I_0 = (b - a) F (\bar x) \Int_{c}^{d} f(\bar x, y) \diff y \approx \newline &\approx (b - a)(d - c) f(\bar x, \bar y), \end{aligned} \end{equation}

де

\begin{equation} \bar = \frac{a + b}{2}, \quad \bar y = \frac{c + d}{2}. \end{equation}

Кубатурна формула (це формула наближеного обчислення інтегралу \eqref{eq:9.9.1}), якщо використовується формула трапеції має вигляд

\begin{equation} \label{eq:8.8.4} \begin{aligned} I &\approx I_1 = \frac{(b - a) (d - c)}{4} \cdot \newline & \quad \cdot (f(a, c) + f(b, c) + f(a, d) + f(b, a)). \end{aligned} \end{equation}

Точність залежить від поведінки функції та від довжини інтервалів $[a,b]$, $[c,d]$. Аналог формул складеного типу для \eqref{eq:9.9.1} будується таким чином: розбиваємо $D$ на комірки:

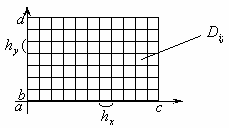
Тоді

\begin{equation} D = \bigsqcup_{i, j} D_{i,j}, \end{equation}

де $D_{i,j} = \{x_{i - 1} \le x \le x_i, y_{j - 1} \le y \le y_j\}$, а у свою чергу $x_i = a + i h_x$ для $i = \overline{0, N_x}$, і $y_j = c+ j h_y$ для $j = \overline{0, N_y}$, і нарешті $h_x = \frac{b - a}{N_x}$ і $h_y = \frac{d - c}{N_y}$.

Тоді для кожного інтегралу по комірці застосовуємо кубатурну формулу прямокутників $(164)$:

\begin{equation} \begin{aligned} I &= \Sum_{i = 1}^{N_x} \Sum_{j = 1}^{N_y} \Iint_{D_{i,j}} f(x, y) \diff x \diff y \approx \newline &\approx I_{0, h} = \Sum_{i = 1}^{N_x} \Sum_{j = 1}^{N_y} h_x h_y f(\bar x_i, \bar y_i), \end{aligned} \end{equation}

де $\bar x_i = x_i - h_x / 2$, а $\bar y_j = y_j - h_y / 2$.

Якщо $f(x, y) \in C^{(2)}(D)$, то $I - I_{0, h} = O(h_x^2 + h_y^2)$. Степінь точності по крокам сітки — $2$. Складність методу пропорційна кількості комірок: $Q = O(N_x N_y ) = O(N^2)$, якщо $N \approx N_x \approx N_y$. В $3$-вимірному просторі $f = f (x, y, z)$ складність — $Q = O(N^3)$.

Якщо $D$ не прямокутник, то замість $f$ введемо

\begin{equation} \bar f(x, y) = \begin{cases} f(x,y), & x \in D, \newline 0, & x \in \Pi \setminus D, \end{cases} \end{equation}

де $\Pi$ — найменший охоплюючий $D$ прямокутник $D \subset \Pi$:

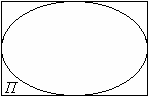
Тоді

\begin{equation} I = \Iint_\Pi \bar f(x, y) \diff x \diff y, \end{equation}

що розглядався вище.

Недолік такого підходу: $f(x, y)$ може бути розривною функцією і через це низька точність обчислення інтегралу.

Наступний підхід базується на відповідній заміні змінних

\begin{equation} x = x(\xi, \eta), \quad y = y(\xi, \eta), \end{equation}

такій, що $D \mapsto \Pi$, тоді

\begin{equation} I = \Iint_\Pi f(x(\xi, \eta), y(\xi, \eta)) J(\xi, \eta) \diff \xi \diff \eta, \end{equation}

де $\Pi$ — прямокутник в площині $(\xi, \eta)$; $J(\xi, \eta)$ — Якобіан переходу. Якщо границя області $D$ гладка, то якобіан буде мати особливості, що також знижує швидкість збіжності.

Ще один підхід в обчисленні інтегралу по довільній області $D$ базується на триангулювання області. Якщо область довільного вигляду, то її можна розбити на трикутники таким чином:

\begin{equation} D = \bigsqcup_{k = 1}^N D_k. \end{equation}

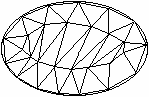
Тоді

\begin{equation} I = \Sum_{k = 1}^{N} I_k, \quad I_k = \Iint_{D_k} f(x, y) \diff x \diff y \end{equation}

Застосуємо кубатурні формули до кожного $I_k \approx I_k^h$. Для цього замінимо функцію поліномом першого степеня

\begin{equation} f(x, y) \approx L_1(x, y) = A + B x + C y. \end{equation}

Задача 35: Побудувати явний вигляд кубатурної формули, яка дозволяє наближено обчислити $I_k$ по трикутнику $D_k$, якщо замінити $f(x, y) \approx L_1(x, y)$ на інтерполяційний багаточлен $1$-го степеня.

Точність такого підходу

\begin{equation} I - I^h = I - \Sum_{k = 1}^{N} I_k^h = O(h^2), \end{equation}

де $h = \Max_k \diam D_k$.

Складність обчислення інтеграла: $Q = O(h^{-2})$ для $D \subset \RR^2$; $Q = O(h^{-3})$ для $D \subseteq \RR^3$.

Можна згустити сітку, поділивши один трикутник $D_k$ на чотири:

І, нарешті, розглянемо ідею методу статистичних випробувань (метод Монте-Карло) для обчислення інтегралу

\begin{equation} I = \Iint_D f(x, y) \diff x \diff y. \end{equation}

Замінимо наближено

\begin{equation} I = \Iint_\Pi \bar f(x, y) \diff x \diff y \approx \frac{1}{N} \Sum_{i = 1}^{N} \bar f(\xi_i, \eta_i) \cdot \mu(\Pi_i), \end{equation}

де $\mu$ — міра нп відповідному просторі, $\Pi$ — найменший охоплюючий $D$ прямокутник $D \subset \Pi$; $f(x, y)$ — продовження функції $f$; $\xi_i$, $\eta_i$ — незалежні реалізації рівномірно розподілених на $[a,b]$ та $[c,d]$ випадкових величин $\xi$ та $\eta$. Складність цього методу $Q = O(N)$. Оцінка точності — $I - I_N = O \left( 1 / \sqrt{N} \right)$ носить ймовірнистний характер.

• Позитивна сторона методу — незалежна від розмірності складність;

• негативна — низька точність.

Назад до лекцій

Назад на головну