6. Інтерполювання функцій

6.1. Постановка задачі інтерполювання

Нехай функція $f(x) \in C([a,b])$ задана своїми значеннями $y_i = f(x_i)$, $x_i \in [a,b]$, $i = \overline{0,n}$, причому $x_i \ne x_j$ для $i \ne j$.

Означення: Функція $\Phi(x)$ називається інтерполюючою для $f(x)$ на сітці $\{x_i\}^n_{i = 0}$, якщо $\Phi(x_i) = y_i$, $i = \overline{0,n}$.

Задача інтерполювання функції має не єдиний розв’язок.

Означення: Виберемо систему лінійно незалежних функцій $\{\varphi_k(x)\}^n_{k = 0}$, $\varphi_k(x) \in C([a,b])$ і побудуємо лінійну комбінацію

\begin{equation} \label{eq:6.1.1} \Phi(x) = \Phi_n(x) = \Sum_{k = 0}^n c_k \cdot \varphi_k(x), \end{equation}

яка називається узагальненим багаточленом.

Умови інтерполювання дають СЛАР

\begin{equation} \label{eq:6.1.2} \Sum_{k = 0}^n c_k \cdot \varphi_k(x_i) = y_i, \quad i = \overline{1, n} \end{equation}

розв’язком якої є $\vec c = (c_0, \ldots, c_n)$.

Якщо

\begin{equation} D(x_0, \ldots, x_n) = \begin{vmatrix} \varphi_0(x_0) & \cdots & \varphi_n(x_0) \newline \vdots & \ddots & \vdots \newline \varphi_0(x_n) & \cdots & \varphi_n(x_n) \end{vmatrix} \ne 0, \end{equation}

то система \eqref{eq:6.1.2} має єдиний розв’язок.

Означення: Система функцій $\{\varphi_k (x)\}^n_{k = 0}$ називається системою Чебишова, якщо $\forall \{x_i\}^n_{i = 0}$ таких, що $x_i \in [a,b]$ і $x_i \ne x_j$ при $i \ne j$ виконується $D(x_0, \ldots, x_n)\ne 0$.

Приклади систем Чебишова:

1. $\varphi_k(x) = x^k$ — алгебраїчна система.

   Визначник $D(x_0, \ldots, x_n) \ne 0$ є визначником Вандермонда:

   \begin{equation} \begin{aligned} D(x_0, \ldots, x_n) &= \begin{vmatrix} 1 & x_0 & \cdots & x_0^n \newline \vdots & \vdots & \ddots & \vdots \newline 1 & x_n & \cdots & x_n^n \end{vmatrix} = \newline &= \Prod_{0 \le k \le m \le n} (x_k - x_m) \ne 0,
   \end{aligned} \end{equation}

2. $\varphi_k (x) = L_k(x)$ — ортогональні багаточлени Лежандра;

3. $\varphi_k(x) = T_k(x)$ — ортогональні багаточлени Чебишова.

4. $\varphi_k(x)$: $1$, $\cos(x)$, $\sin(x)$, $\ldots$, $\cos(nx)$, $\sin(nx)$.

   Тоді

   \begin{equation} \begin{aligned} \Phi_n(x) &= T_n(x) = \newline &= a_0 + \Sum_{k = 1}^n (a_k \cdot \cos(k x) + b_k \cdot \sin(k x)) \end{aligned} \end{equation}

   — тригонометричний багаточлен.

6.2. Інтерполяційна формула Лагранжа

Якщо $\varphi_k(x) = x^k$, то

\begin{equation} \Phi_n(x) = P_n(x) = \Sum_{k=0}^n c_k \cdot x^k. \end{equation}

Задача інтерполювання функції $f(x)$ алгебраїчним, багаточленом полягає в знаходженні коефіцієнтів $c_k$, $k = \overline{0,n}$ для яких виконується умова $f(x_i) = \varphi(x_i)$, $i = \overline{0, n}$.

Представимо інтерполяційний багаточлен у вигляді

\begin{equation} \label{eq:6.2.1} P_n(x) = L_n(x) = \Sum_{k = 0}^n f(x_k) \cdot \Phi_k^{(n)}(x). \end{equation}

Означення: Тут $L_n(x)$ — інтерполяційний поліном; $\Phi_k^{(n)}(x)$ — поліноми $n$-го степеня, які називають множниками Лагранжа.

З умови $L_n(x_i) = f(x_i)$ випливає, що множник Лагранжа повинен задовольняти умови

\begin{equation} \label{eq:6.2.2} \Phi_k^{(n)} (x_i) = \delta_{i,k}. \end{equation}

Оскільки $\Phi_k^{(n)}(x)$ — багаточлен степеня $n$, то він має вигляд

\begin{equation} \Phi_k^{(n)}(x) = A_k (x - x_0) \ldots (x - x_{k-1}) (x - x_{k+1}) \ldots (x - x_n), \end{equation}

де $A_k$ — число.

Знайдемо його з умови $\Phi_k^{(n)}(x_k) = 1$:

\begin{equation} A_k = \frac{1}{(x_k - x_0) \ldots (x_k - x_{k-1}) (x_k - x_{k + 1}) \ldots (x_k - x_n)}. \end{equation}

Таким чином багаточлен $\Phi_k^{(n)}(x)$ мають вигляд:

\begin{equation} \label{eq:6.2.3} \Phi_k^{(n)} (x) = \frac{(x - x_0) \ldots (x - x_{k-1}) (x - x_{k+1}) \ldots (x - x_n)}{(x_k - x_0) \ldots (x_k - x_{k-1}) (x_k - x_{k+1}) \ldots (x_k - x_n)} \end{equation}

Позначивши

\begin{equation} \omega_n(x) = \Prod_{i = 0}^n(x - x_i), \end{equation}

маємо

\begin{equation} \Phi_k^{(n)}(x) = \frac{\omega_n(x)}{(x - x_k) \cdot \omega_n’(x_k)}. \end{equation}

Остаточно формула Лагранжа має вигляд

\begin{equation} \label{eq:6.2.4} L_n(x) = \Sum_{k = 0}^n f(x_k) \cdot \frac{\omega_n(x)}{(x - x_k) \cdot \omega_n’(x_k)} \end{equation}

6.3. Залишковий член інтерполяційного полінома

В заданих точках (точки інтерполювання) значення функції та полінома співпадають, але в інших точках в загальному випадку не співпадають. Отже доцільно розглянути питання про похибку інтерполювання.

Означення: Замінюючи функцію $f(x)$ на $L_n(x)$ ми допускаємо похибку $r_n(x) = f(x) - L_n(x)$. Це залишковий член інтерполювання.

З означення випливає, що, $r_n(x_i) = 0$, $x_i \in [a,b]$. Оцінимо похибку у кожній точці $x \in [a,b]$. Введемо допоміжну функцію:

\begin{equation} g(t) = f(t) - L_n(t) - K \cdot \omega_n(t), \end{equation}

де $t \in [a,b]$, і $g(x_i) = 0$ для $i = \overline{0,n}$.

Знайдемо таке $K$, щоб $g(x) = 0$, в деякій точці $x \in [a,b]$, $x \ne x_i$, $i = \overline{0,n}$. Легко бачити, що

\begin{equation} K = \frac{f(x) - L_n(x)}{\omega_n(x)}. \end{equation}

Припустимо що $f(x) \in C^{(n+1)}([a,b])$, тоді $g(t) \in C^{(n+1)}([a,b])$. Функція $g(t) = 0$ в $(n + 2)$-х точках, а саме $t = x$, $t = x_i$, $i = \overline{0,n}$. З теореми Ролля випливає, що існує $(n+1)$-а точка, де $g'(t_i)=0$, $i = \overline{0,n}$. Продовжуючи цей процес, отримаємо, що існує хоча б одна $\xi \in [a,b]$ така, що $g^{(n+1)} (\xi) = 0$. Оскільки

\begin{equation} g^{(n+1)}(t) = f^{(n+1)} - 0 - K \cdot (n+1)!, \end{equation}

то $\exists \xi$, що

\begin{equation} g^{(n+1)}(\xi) = f^{(n+1)}(\xi) - (n+1)! \cdot \frac{f(x) - L_n(x)}{\omega_n(x)} = 0. \end{equation}

Звідси

\begin{equation} \label{eq:6.3.1} r_n(x) = f(x) - L_n(x) = \frac{f^{(n+1)}(\xi)}{(n + 1)!} \cdot \omega_n(x). \end{equation}

Оскільки $\xi$ невідомо, то використовують оцінку залишкового члена:

\begin{equation} \label{eq:6.3.2} |r_n(x)| = |f(x) - L_n(x)| \le \frac{M_{n + 1}}{(n + 1)!} \cdot |\omega_n(x)|, \end{equation}

де $M_{n + 1} = \Sup_{x \in [a,b]} \vert f^{(n+1)}(x) \vert$.

6.4. Багаточлени Чебишова. Мінімізація залишкового члена інтерполяційного полінома

Як вибрати вузли інтерполяції щоб похибка інтерполювання була мінімальною? Спочатку обґрунтуємо теоретичний апарат, завдяки якому будемо досліджувати це питання.

Означення: Багаточленом Чебишова ($n$-того степеня, 1–го роду) називається поліном, який задається такими рекурентними співвідношеннями

\begin{equation} \label{eq:6.4.1} T_{n + 1}(x) - 2 x \cdot T_n(x) + T_{n - 1}(x) = 0, \end{equation}

де початкові значення

\begin{equation} \label{eq:6.4.2} T_0(x) = 1, \quad T_1(x) = x. \end{equation}

Знайдемо явний вигляд багаточлена Чебишова. Будемо шукати розв’язок рівняння \eqref{eq:6.4.1} у вигляді $T_n(x) = q^n$, де $q = q(x)$. Підставивши в \eqref{eq:6.4.1}, отримуємо характеристичне рівняння $q^2 - 2 x q + 1 = 0$. Тоді при $\vert x \vert \ge 1 \implies q_{1,2} = x \pm \sqrt{x^2 - 1}$, а при $\vert x \vert < 1 \implies q_{1,2} = \cos(\varphi) \pm i \sin(\varphi)$, $\varphi = \arccos(x)$.

Розглянемо обидва випадки детальніше:

1. при $\vert x \vert \le 1$: $T_n(x) = A \cdot \cos(n \varphi) + B \cdot \sin (n \varphi)$. З \eqref{eq:6.4.1} випливає $A = 1$, $B = 0$ і тому

   \begin{equation} \label{eq:6.4.3} T_n(x) = \cos(n \arccos (x)). \end{equation}

2. при $\vert x \vert > 1$:

   \begin{equation} \label{eq:6.4.4} T_n(x) = \frac{1}{2} \left( \left(x + \sqrt{x^2 - 1}\right)^n + \left(x - \sqrt{x^2 - 1} \right)^n \right). \end{equation}

Знайдемо нулі та екстремуми багаточлена Чебишова: $T_n(x) = 0$, $x \in [-1,1]$, $\cos(n \arccos(x)) = 0$, $\arccos(x) = \frac{2 k + 1}{2 n} \pi$, $k = \overline{0,n-1}$.

Отже нулі багаточлена Чебишова:

\begin{equation} x_k = \cos \left( \frac{(2 k + 1) \pi}{2 n} \right) \in [-1,1], \quad k = \overline{0,n-1}. \end{equation}

Локальні екстремуми багаточлена Чебишова на $x \in [-1,1]$:

\begin{equation} x_k’ = \cos \left( \frac{k\pi}{2n} \right), \quad k = \overline{0,n}. \end{equation}

Коефіцієнт при старшому члені багаточлена дорівнює $2^{n-1}$.

Означення: Введемо нормований багаточлен Чебишова $\overline T_n(x) = 2^{1-n} T_n(x) = x^n + \ldots$.

Тоді

\begin{equation} \left| \overline T_n \right|\void_{C([-1,1])} = \Max_{x \in [-1,1]} |T_n(x)| = 2^{1-n}. \end{equation}

Означення: Відхиленням двох функцій $f(x)$ та $\Phi(x)$ називається величина

\begin{equation} \Delta (f, \Phi) = | f(x) - \Phi(x)|\void_{C([a,b])}. \end{equation}

Теорема (Чебишова): Серед усіх багаточленів $n$-го степеня з коефіцієнтом $1$ при старшому степені $\overline T_n(x)$ найменше відхиляється від $0$ на $[-1,1]$, тобто

\begin{equation} \left|\overline T_n(x) - 0 \right|\void_{C([-1,1])} = \Inf_{\overline P_n(x)} \left|\overline P_n(x)\right|\void_{C([-1,1])} = 2^{1-n}. \end{equation}

Доведення: Будемо доводити від супротивного: припустимо, що існує багаточлен, такий, що

\begin{equation} \overline Q_n(x) < 2^{1-n}. \end{equation}

Тоді $Q_{n-1}(x) = \overline T_n(x) - \overline Q_n(x)$ — поліном степеня не вище $n - 1$ і не рівний тотожньо нулю. Дослідимо його знаки:

\begin{equation} \sign \left( Q_{n - 1}(x_k’) \right) = \sign \left( \overline T_n(x_k’) - \overline Q_n(x_k’) \right) = \sign \left( \overline T_n(x_k’) \right) = \alpha \cdot(-1)^k, \end{equation}

де $\alpha = \pm 1$.

Значить $\exists z_k$, $k = \overline{0,n-1}$ таке, що $Q_{n-1}(z_k)=0$. Це протиріччя, бо $Q_{n-1}(x)$ — поліном степеня $\le n - 1$. $\square$

Тепер узагальнимо наш багаточлен Чебишова на довільний проміжок. Нагадаємо $T_n(t) = \cos(n \arccos t)$, $-1 \le t \le 1$. Від змінної $t \in [-1, 1]$ перейдемо до $x \in [a,b]$. Запровадимо заміну

\begin{equation} t = \frac{2 x}{b - a} - \frac{b + a}{b - a}, \quad x = \frac{b + a}{2} + \frac{b - a}{t}. \end{equation}

Тоді

\begin{equation} T_n^{[a,b]}(t) = \overline T_n \left( \frac{2 x}{b - a} - \frac{b + a}{b - a} \right) = 2^{1 - n} \cos \left(n \arccos \left( \frac{2 x - (b + a)}{b - a} \right) \right). \end{equation}

Побудований нами багаточлен Чебишова на $[a,b]$ не є нормованим.

Нормований багаточлен Чебишова на $[a,b]$:

\begin{equation} \overline T_n^{[a,b]}(x) = \frac{(b - a)^n}{2^{2 n - 1}} \cos \left(n \arccos \left( \frac{2 x - (b + a)}{b - a} \right) \right). \end{equation}

Відповідно його нулі

\begin{equation} x_k = \frac{a + b}{2} - \frac{b - a}{2} \cdot t_k, \quad t_k = \cos \left( \frac{(2 k + 1) \pi}{2 n} \right), \end{equation}

де $k = \overline{0,n-1}$, а точки екстремуму

\begin{equation} x_k’ = \frac{a + b}{2} - \frac{b -a }{2} \cdot t_k’, \quad t_k’ = \cos \left( \frac{k \pi}{n} \right), \quad k = \overline{0,n}. \end{equation}

Теорема Чебишова вірна і у випадку $[a,b]$. Тепер

\begin{equation} \left|\overline T_n^{[a,b]}\right|\void_{C([a,b])} = \frac{(b-a)^n}{2^{2n-1}}. \end{equation}

Перейдемо до питання мінімізації залишкового члена. Нагадаємо, що

\begin{equation} \label{eq:6.4.5} |r_n(x)| = |f(x) - L_n(x)| \le \frac{M_{n + 1}}{(n + 1)!} \cdot |\omega_n(x)|, \end{equation}

де $M_{n + 1} = \Max_{x \in [a,b]} \left\vert f^{(n+1)}(x) \right\vert$, $\omega_n(x) = \Prod_{i = 0}^n (x - x_i) = x^{n+1} + \ldots$

Поставимо задачу

\begin{equation} \Inf_{\overline P_n(x)} \Max_{x \in [a,b]} |\omega_n(x)|. \end{equation}

З теоремою Чебишова $\omega_n(x) = \overline T_{n+1}^{[a,b]}(x)$ поліном Чебишова. Якщо співпадають поліноми, то співпадають їх нулі. Отже: $x_k$ — вузли інтерполяції співпадають з нулями багаточлена Чебишова

\begin{equation} x_k = \frac{a + b}{2} - \frac{b - a}{2} \cdot t_k, \quad t_k = \cos \left( \frac{(2 k + 1) \pi}{2 (n + 1)} \right), \end{equation}

де $k = \overline{0,n}$.

В цьому випадку

\begin{equation} \label{eq:6.4.6} |r_n(x)| = |f(x) - L_n(x)| \le \frac{M_{n + 1}}{(n + 1)!} \cdot \frac{(b - a)^{n + 1}}{2^{2 n + 1}}. \end{equation}

Цю оцінку не можна покращити! Так для $f(x) = \overline P_{n + 1}(x) = x^{n + 1} + \ldots$ її $(n + 1)$ похідна дорівнює $(n + 1)!$, тому $M_{n + 1} = (n + 1)!$. Різниця $f(x) - L_n(x) = \overline T_{n + 1}^{[a,b]}(x)$, отже

\begin{equation} \Max_{x \in [a,b]} |f(x) - L_n(x)| = \frac{(b - a)^{n + 1}}{2^{2 n + 1}}. \end{equation}

6.5. Розділені різниці

Розділені різниці є аналогом похідної для функції, що задана таблицею.

Означення: Розділеною різницею 1-го порядку для функції $f(x)$ називатимемо

\begin{equation} f(x_i; x_j) = \frac{f(x_i) - f(x_j)}{x_i - x_j}. \end{equation}

Розділеною різницею 2-го порядку для функції $f(x)$ називатимемо

\begin{equation} f(x_i; x_j; x_k) = \frac{f(x_i; x_j) - f(x_j; x_k)}{x_i - x_k}. \end{equation}

Аналогічно визначаються розділені різниці довільного порядку.

Наведемо деякі властивості розділених різниць:

1. \begin{equation} f(x_0; \ldots; x_n) = \Sum_{i = 0}^n \frac{f(x_j)}{\Prod_{i \ne j}(x_i - x_j)}. \end{equation}

2. Розділена різниця — лінійний функційонал:

   \begin{equation} (\alpha_1 f_1 + \alpha_2 f_2)(x_0; x_1) = \alpha_1 f_1(x_0;x_1) + \alpha_2 f_2(x_0;x_1). \end{equation}

3. Розділена різниця — симетричний функціонал:

   \begin{equation} f(x_1; \ldots; x_i; \ldots; x_j; \ldots; x_n) = f(x_1; \ldots; x_j; \ldots; x_i; \ldots; x_n). \end{equation}

4. $\forall f(x) \in C^{(n)}([a,b])$: $\exists \xi \in [a,b]$: $f(x_0; x_1; \ldots; x_n) = \frac{f^{(n)}(\xi)}{n!}$.

Задача 14: Довести першу властивість розділених різниць.

Таблиця розділених різниць має вигляд:

$x_i$	$f_i$	р.р.$1$	р.р.$2$	$\ldots$	р.р.$n$
$x_0$	$f(x_0)$
		$f(x_0;x_1)$
$x_1$	$f(x_1)$		$f(x_0;x_1;x_2)$
		$f(x_1;x_2)$
$x_2$	$f(x_2)$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$f(x_0;\ldots;x_n)$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_{n-2}$	$f(x_{n-2})$
		$f(x_{n-2};x_{n-1})$
$x_{n-1}$	$f(x_{n-1})$		$f(x_{n-2};x_{n-1};x_n)$
		$f(x_{n-1};x_n)$
$x_n$	$f(x_n)$

6.6. Інтерполяційна формула Ньютона

Запишемо формулу Лагранжа інтерполяційного багаточлена

\begin{equation} \label{eq:6.6.1} L_n(x) = \Sum_{i = 0}^n f(x_i) \cdot \frac{\omega_n(x)}{(x - x_i) \cdot \omega_n’(x_i)}, \end{equation}

де $\omega_n(x) = \Prod_{j=0}^n (x-x_j)$.

Позначимо $\Phi_j(x) = L_j(x) - L_{j-1}(x)$. Тоді, оскільки

\begin{equation} L_n(x) = L_0(x) + (L_1(x) - L_0(x)) + \ldots + (L_n(x) - L_{n-1}(x)), \end{equation}

і

\begin{equation} L_j(x_i) = L_{j-1}(x_i) = f(x_i), \quad i = \overline{0,j-1}, \end{equation}

то \begin{equation} \label{eq:6.6.2} \Phi_j(x_i) = A_j \cdot (x - x_0) \cdot \ldots \cdot (x - x_{j-1}), \end{equation}

де $A_j$ визначається з умови $\Phi_j(x_j) = L_j(x_j) - L_{j-1}(x_j) = f(x_j) - L_{j-1}(x_j)$. Звідси

\begin{equation} \Phi_j(x) = \frac{f(x_j) - L_{j-1}(x_j)}{(x_j - x_0) \ldots (x_j - x_{j - 1})} \cdot (x-x_0) \ldots (x-x_j). \end{equation}

Тоді \begin{equation} \begin{aligned} A_j &= \frac{f(x_j) - L_{j-1}(x_j)}{(x_j - x_0) \ldots (x_j - x_{j-1})}= \frac{f(x_j)}{(x_j - x_0) \ldots (x_j - x_{j-1})} - \newline & \quad - \Sum_{i = 0}^{j - 1} \frac{f(x_i)}{(x_i - x_0) \ldots (x_i - x_{i-1}) (x_i - x_{i + 1}) \ldots (x_j-x_i)} = \newline & = \frac{f(x_j)}{(x_j-x_0) \ldots (x_j - x_{j-1})} + \Sum_{i = 0}^{j - 1} \frac{f(x_i)}{(x_i-x_0) \ldots (x_i - x_j)} = \newline & = \Sum_{i = 0}^j \frac{f(x_i)}{(x_i - x_0) \ldots (x_i - x_{i - 1}) (x_i - x_{i + 1}) \ldots (x_i - x_j)} = f(x_0;\ldots;x_j). \end{aligned} \end{equation}

Звідси маємо інтерполяційну формулу Ньютона вперед ($x_0 \to x_n$):

\begin{equation} \label{eq:6.6.3} L_n(x) = f(x_0) + f(x_0;x_1) (x-x_0) + \ldots + f(x_0;\ldots;x_n) (x-x_0) \ldots (x - x_{n-1}). \end{equation}

Аналогічно, інтерполяційна формула Ньютона назад ($x_n\to x_0$): \begin{equation} \label{eq:6.18} L_n(x) = f(x_n) + f(x_n;x_{n-1}) (x-x_n) + \ldots + f(x_n;\ldots;x_0) (x-x_n) \ldots (x-x_1). \end{equation}

Маємо рекурсію за степенем багаточлена

\begin{equation} L_n(x) = L_{n-1}(x) + f(x_0;\ldots;x_n) (x-x_0) \ldots (x-x_1). \end{equation}

Звідси

\begin{equation} L_n(x) = f(x_0) + (x - x_0) (f(x_0;x_1) + (x - x_1) (\ldots + (x - x_{n-1}) f(x_0;x_1;\ldots;x_n) \ldots )) \end{equation}

і цю формулу розкриваємо починаючи з середини (це аналог схеми Горнера обчислення значення багаточлена).

Введемо нову формулу для похибки інтерполювання. Для $x \ne x_i$, $i = \overline{0,n}$ розглянемо розділену різницю

\begin{equation} f(x; x_0; \ldots; x_n) = \frac{f(x)}{(x - x_0) \ldots (x - x_n)} + \Sum_{k = 0}^n \frac{f(x_k)}{\Prod_{i \ne k}(x - x_i)}. \end{equation}

Звідси

\begin{equation} \begin{aligned} f(x) &= f(x_0) \cdot \frac{(x - x_1) \ldots (x - x_n)}{(x_0 - x_1) \ldots (x_0 - x_n)} + \ldots + f(x_n) \cdot \frac{(x - x_1) \ldots (x - x_n)}{(x_n - x_1) \ldots (x_n - x_{n-1})} + \newline & \quad + f(x; x_0; \ldots; x_n) (x - x_0) \ldots (x - x_n) = L_n(x) + f(x; x_0; \ldots; x_n) \cdot \omega_n(x). \end{aligned} \end{equation}

Тоді похибка має вигляд \begin{equation} \label{eq:6.19} r_n(x) = f(x) - L_n(x) = f(x;x_0;\ldots;x_n)\cdot\omega_n(x). \end{equation}

Це нова форма для залишкового члена.

Порівнюючи з формулою залишкового члена в пункті $6.3$, маємо

\begin{equation} f(x; x_0; \ldots; x_n) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}, \end{equation}

що доводить останню властивість розділених різниць.

Нехай маємо сітку рівновіддалених вузлів: $x_i = a + i h$, $h = \frac{b-a}{n}$, $i = \overline{0, n}$, $x_0 = a$, $x_n = b$. Розначимо $\Delta f_0 = f_1 - f_0$, $\Delta^2f_0 = \Delta f_1 - \Delta f_0 = f_2 - 2 f_1 + f_0$, $\ldots$ — скінченні різниці.

Запишемо формули Ньютона у нових позначеннях:

\begin{equation} L_n(x) = L_n(x_0 + t h) = f_0 + t \Delta f_0 + \ldots + \frac{t (t - 1) \ldots (t - n + 1)}{n!}\cdot \Delta^n f_0, \end{equation}

де $t = \frac{x-x_0}{h}$.

Це інтерполяційна формула Ньютона вперед по рівновіддалених вузлах.

Задача 15: Побудувати інтерполяційну формулу Ньютона назад по рівновіддалених вузлах.

6.7. Інтерполювання з кратними вузлами

Нехай $f(x)$ задана таблицею значень $f^{(j)}(x_i)$, $i = \overline{0, n}$, $j = \overline{0, k_i - 1}$, $k_i$ — кратності відповідних вузлів. Побудуємо $H_m^{(i)}(x_j) = f^{(i)}(x_j)$ — інтерполяційний багаточлен Ерміта по кратним вузлах, де

\begin{equation} m = \Sum_{i = 1}^n k_i - 1. \end{equation}

Якщо $k_i = 1$, то $H_m(x) = L_n(x)$.

Для побудови $H_m(x)$ в загальному випадку для кожної точки $x_i$ введемо $k_i$ точок $x_{i, j}^\varepsilon = x_i + j \varepsilon$, $i = \overline{0, n}$, $j = \overline{0, k_i - 1}$. З умови $\forall i$: $x_{i, k_i - 1}^\varepsilon = x_i + \varepsilon (k - 1) < x_{i + 1}$ можна вибрати $\varepsilon$.

Нехай $f(x) \in C^{(m)}([a,b])$. Запишемо інтерполяційну формулу Ньютона:

\begin{equation} \begin{aligned} L_m^\varepsilon &= f \left( x_{0, 0}^\varepsilon \right) + f \left(x_{0, 0}^\varepsilon; x_{0, 1}^\varepsilon \right) \left(x - x_{0, 0}^\varepsilon \right) + \ldots \newline & \quad + f \left( x_{0, 0}^\varepsilon; \ldots; x_{n, k_n - 1}^\varepsilon \right) \left( x - x_{0, 0}^\varepsilon \right) \ldots \left( x - x_{n, k_n - 1}^\varepsilon \right). \end{aligned} \end{equation}

При $\varepsilon \to 0$ маємо $x_{i,j}^\varepsilon \to x_i$. Крім того

\begin{equation} f \left( x_{i,0}^\varepsilon; \ldots; x_{i, k_i - 1}^\varepsilon \right) = f (x_i; \ldots; x_i) = \frac{f^{(k_i)}(x_i)}{k_i!}. \end{equation}

Тому $L_m^\varepsilon(x) \to H_m(x)$ та

\begin{equation} R_m(x) = f(x) - H_m(x) = \frac{f^{(m + 1)}(\xi)}{(m + 1)!} \cdot \Omega_m(x), \end{equation}

де $\Omega_m(x) = (x - x_0)^{k_0} \ldots (x - x_n)^{k_n}$.

6.8. Збіжність процесу інтерполювання

Виникає питання, чи буде прямувати до нуля похибка інтерполювання $f(x) - L_n(x)$, якщо число вузлів $n$ збільшувати?

Введемо норму

\begin{equation} |f(x) - L_n|\void_{C([a,b])} = \Max_{x \in [a,b]} | f(x) - L_n(x) |. \end{equation}

Тоді для довільної $f(x) \in C^{(n + 1)}([a,b])$ справджується оцінка

\begin{equation} \label{eq:6.8.1} | f(x) - L_n(x)|\void_{C([a,b])} \le \frac{M_{n + 1}}{(n + 1)!} |\omega_n(x)|\void_{C([a,b])}, \end{equation}

де $M_{n + 1} = \Max_{x \in [a,b]} \left\vert f^{(n + 1)}(x) \right\vert$, $\omega_n(x) = \Prod_{i = 0}^n (x - x_i)$.

А яка оцінка буде для довільної неперервної функції?

Означення: Кажуть, що інтерполяційний процес для функції $f(x)$ збігається в точці $x \in [a,b]$, якщо

\begin{equation} \forall \{x_i\}^n_{i = 1}: h = \Max_{i = \overline{1,n}} \to 0: \Lim_{n\to\infty} L_n(x) = f(x), \end{equation}

де, як завжди, $h_i = x_i - x_{i-1}$.

Означення: Якщо $\|f(x) - L_n(x)\|\void_{C([a,b])} \xrightarrow[n\to\infty]{}0$, то інтерполяційний процес збігається рівномірно.

Розглянемо приклади поведінки інтерполяційних багаточленів при $n \to \infty$ для деяких функцій.

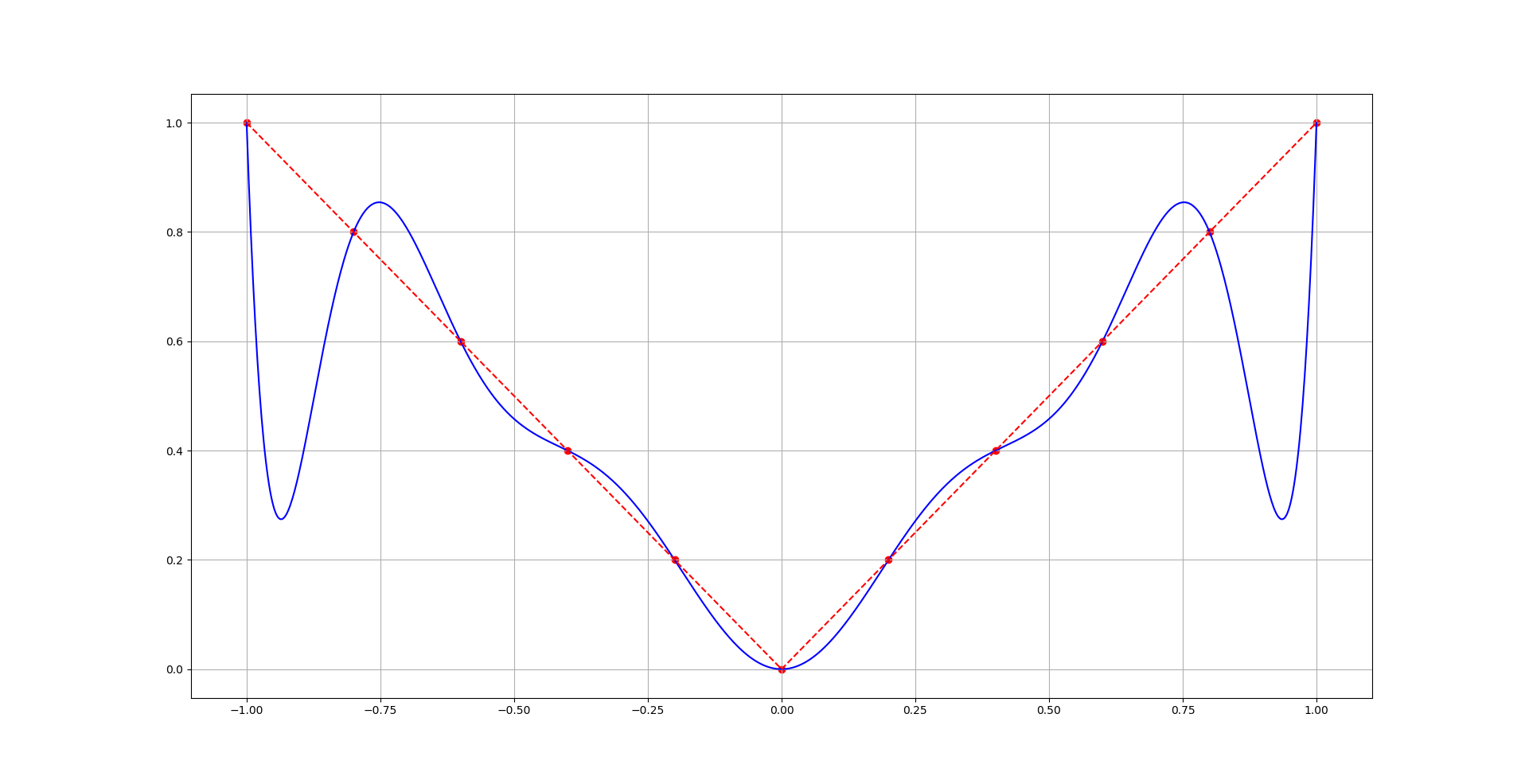
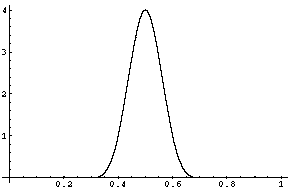
Приклад 1: Послідовність інтерполяційних багаточленів (сітка рівномірна), побудованих для неперервної функції $f(x) = \vert x \vert$, $-1 \le x \le 1$ (функція неперервна, але негладка), не збігається на $x \in [-1,1]$, крім точок $x = -1,0,1$.

На рисунку дано графіки самої функції (штрихова лінія) та інтерполяційного багаточлена (суцільна лінія) на рівномірній сітці $x_i = -1 + i h$, $h = 2 / n$, $i = \overline{0,n}$ для $n = 10$:

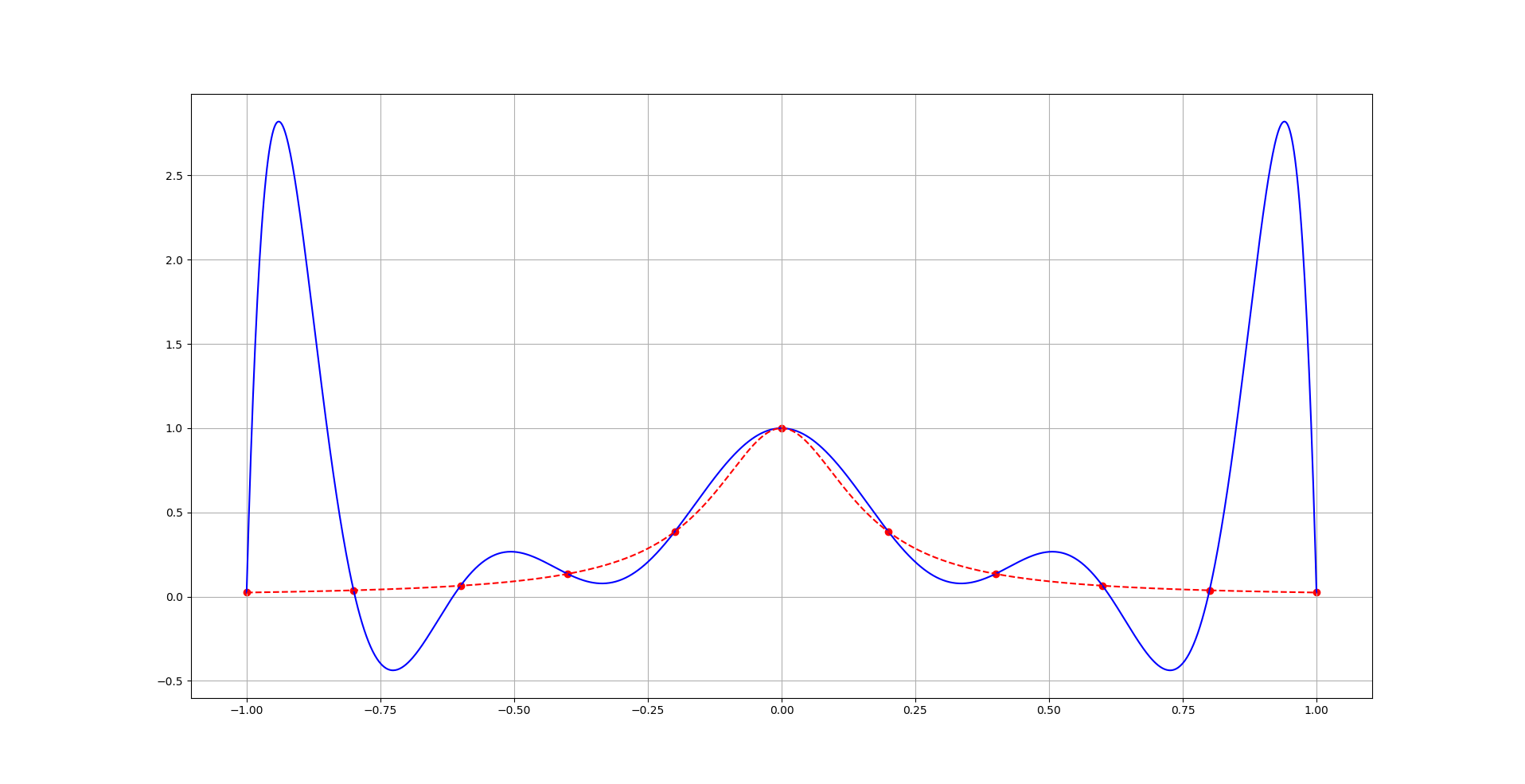
Приклад 2: Функція Рунге $f(x) = \frac{1}{1 + 40x^2}$, $-1 \le x \le 1$ (функція аналітична!). Для рівномірної сітки $x_i = -1 + i h$, $h = 2 / n$, $i = \overline{0,n}$ маємо графіки: суцільна лінія — інтерполяційного багаточлена; пунктирна — самої функції для $n = 10$:

Пояснити чому рівномірна сітка дає великі похибки інтерполювання біля кінців інтервалу інтерполювання допомагає наступний рисунок. На цьому рисунку суцільною лінією представлено графік функції $\omega_n = \Prod_{i = 0}^n (x - x_i)$ ($n = 8$) для рівномірної сітки. Як бачимо максимальні за модулем значення цієї функції припадають на кінці інтервалу.

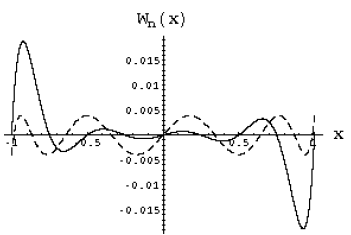
Для порівняння на цьому ж рисунку (штрихова лінія) побудовано графік $\omega_n = \Prod_{i = 0}^n (x - x_i)$, що відповідає чебишовським вузлам, які мінімізують похибку інтерполювання. Тепер відхилення $\omega_n(x)$ розподілено рівномірно по всьому проміжку інтерполювання.

Теорема (Фабера): $\forall \{x_i\}^n_{i = 0}$ існує $f(x) \in C([a,b])$, для якої інтерполяційний процес не збігається рівномірно.

Теорема (Марцинкевича): $\forall f(x) \in C([a,b])$ існуюють $\{x_i\}^n_{i = 0}$ такі, що послідовність $\{L_n(x)\}$ збігається рівномірно до $f(x)$.

Теорема: Стала Лебега

\begin{equation} |P_n| = \Max_j \Sum_{j = 0}^n \left\vert \varphi_j^{(n)}(x) \right\vert, \end{equation}

де

\begin{equation} \varphi_j^{(n)}(x) = \frac{\omega_n(x)}{(x-x_j) \cdot \omega_n’(x_i)}. \end{equation}

Теорема: Для $f(x) \in C([a,b])$:

\begin{equation} |f(x)-L_n(x)|\void_{C([a,b])} \le (1 + |P_n|) \cdot E_n(f), \end{equation}

де

\begin{equation} E_n(f) = \Inf_{Q_n(x)} |f(x) - Q_n(x)|\void_{C([a,b])} \end{equation}

— відхилення багаточлена $n$-го степеня найкращого рівномірного наближення від $f(x)$.

Теорема: Нехай $P_n^E$ — оператор інтерполяції на рівномірній сітці, $P_n^T$ — оператор інтерполяції на чебишовській сітці. Тоді на $[-1,1]$ маємо наближені оцінки:

\begin{equation} |P_n^E|\approx C_1 \cdot 2^n, \quad |P_n^T| \approx C_2 \cdot \ln(n). \end{equation}

Останні оцінки поясняють розбіжність процесу інтерполювання при великих $n$.

6.9. Кусково-лінійна інтерполяція

Інтерполяція багаточленом Лагранжа або Ньютона на відрізку $[a,b]$ з використанням великої кількості вузлів інтерполяції часто приводить до поганого наближення через розбіжність процесу інтерполювання. Для того щоб уникнути великої похибки, весь відрізок $[a,b]$ розбивають на частинні відрізки $[x_{i-1}, x_i]$ і на кожному з частинних відрізків замінюють функцію $f(x)$ багаточленом невисокого степеню. В цьому і полягає кусково-поліноміальна інтерполяція.

Розглянемо найпростішу таку інтерполяцію — лінійну. Нехай задана $f(x)$ значеннями $f(x_i)$, $i = \overline{0, n}$. Побудуємо функцію $\Phi_1(x)$ — лінійну на $x \in [x_{i - 1}, x_i]$, що інтерполює ці значення:

\begin{equation} \label{eq:6.9.2} \Phi_1(x) = L_1^i(x) = f(x_{i - 1}) \cdot \frac{x - x_{i - 1}}{x_i - x_{i - 1}} + f(x_i) \cdot \frac{x_i - x}{x_i - x_{i - 1}}, \end{equation}

де $x \in [x_{i - 1}, x_i]$.

Представимо її у вигляді

\begin{equation} \label{eq:6.9.3} \Phi_1(x) = \Sum_{i = 0}^n f(x_i) \cdot \varphi_i(x). \end{equation}

З умов інтерполювання маємо

\begin{equation} \Phi_1(x_j) = \Sum_{i = 0}^n f(x_i) \cdot \varphi_i(x_j) = f(x_j). \end{equation}

Звідси

\begin{equation} \varphi_i(x_j) = \delta_{i,j} = \begin{cases} 1, & i = j \newline 0, & i \ne j \end{cases}. \end{equation}

Значить

\begin{equation} \varphi_i(x) = \begin{cases} 0, & a \le x \le x_{i-1} \newline \frac{x-x_{i-1}}{x_i-x_{i-1}}, & x_{i-1} \le x \le x_i \newline \frac{x_{i+1}-x}{x_{i+1}-x_i}, & x_i \le x \le x_{i+1} \newline 0, & x_{i+1} \le x \le b \end{cases} \end{equation}

Теорема: Для довільної $f(x) \in C^{(2)}([a,b])$ справедлива оцінка

\begin{equation} \label{eq:6.9.4} |f(x)-\Phi_1(x)|\void_{C([a,b])} \le \frac{M_2}{8} \cdot |h|^2, \end{equation}

де $\Phi_1(x)$ — кусково-лінійна функція, побудована по значеннях $f(x_i)$, $i = \overline{0, n}$, $\vert h \vert = \Max_i h_i$, $h_i = x_i - x_{i-1}$.

Доведення: Маємо для $x \in [x_{i-1}, x_i]$:

\begin{equation} z(x) = f(x) - \Phi_1(x) = f(x) - L_1^i(x) = \frac{f^{\prime\prime}(\xi_i)}{2!} \cdot (x-x_{i-1}) \cdot(x-x_i). \end{equation}

Звідси

\begin{equation} \label{eq:6.9.5} |f(x) - \Phi_1(x)| \le \frac{M_2^i}{2} \cdot |(x - x_{i-1}) (x - x_i)| \le \frac{M_2^i \cdot h_i^2}{8}, \end{equation}

де

\begin{equation} M_2^i = \Max_{x \in [x_{i - 1}, x_i]} | f^{\prime\prim (x) |. \end{equation}

Остання оцінка отримана з нерівності

\begin{equation} \Max_{[x_{i-1},x_i]} |(x-x_{i-1}) \cdot (x - x_i)| = \frac{h_i^2}{4}. \end{equation}

Тоді

\begin{equation} \label{eq:6.9.6} \Max_{i = \overline{1,n}} \Max_{x \in [x_{i-1},x_i]} |z(x)| \le \frac{h^2 M_2}{8}, \end{equation}

де $M_2 = \Max_{x\in[a,b]} \vert f^{\prime\prime}(x) \vert$, $h_i = \Max_i h_i$, що доводить \eqref{eq:6.9.4}. $\square$

Задача 16: Довести оцінку $\vert f'(x) - \Phi_1'(x) \vert \le \vert h \vert \cdot M_2$.

Отже маємо збіжність процесу інтерполювання за допомогою кусково-лінійної функції

\begin{equation} \left| f(x) - \Phi_1^{(n)}(x) \right|\void_{C([a,b])} \xrightarrow[h \to 0, n \to \infty]{} 0, \end{equation}

тобто

\begin{equation} \left\{\Phi_1^{(n)}(x)\right\} \implies f(x). \end{equation}

Розглянемо деякі простори:

1. $H_0 = L_2([a,b])$ — гільбертів простір, в якому скалярний добуток визначається так:

   \begin{equation} \langle u, v \rangle = \Int_a^b (u(x) \cdot v(x)) \diff x \end{equation}

   а норма $\|u\|\void_0 = \sqrt{\langle u,u \rangle}$.

2. $H_k = W_2^k([a,b])$. Тепер скалярний добуток

   \begin{equation} \langle u, v \rangle_k = \Sum_{m = 0}^k \Int_a^b \left( u^{(m)}(x) \cdot v^{(m)}(x) \right) \diff x, \end{equation}

   а норма $\|u\|\void_k = \sqrt{\|u^{(0)}\|^2 + \ldots + \|u^{(k)}\|^2}$.

Теорема: Нехай $f(x) \in H_2 = W_2^2([a,b])$. Тоді

\begin{equation} \left|f^{(k)} - \Phi_1^{(k)} \right|\void_0 \le \vert h \vert^{2-k} \cdot |f|\void_2, \end{equation}

де $k=1,2$.

Зауважимо, що кусково-лінійна інтерполяція негладка, тому на практиці застосовують квадратичні, а найчастіше — кубічні поліноми на кожному проміжку.

6.10. Кусково-кубічна ермітова інтерполяція

Нехай деяка функція $f(x)$ задана в точках $x_i$ своїми значеннями та значеннями похідної: $y_i = f(x_i)$, $y_i' = f'(x_i)$, $i = \overline{0, n}$. Позначимо через $\Phi_3(x)$ функцію, яка буде інтерполювати задану. Тоді

\begin{equation} \label{eq:6.10.1} \Phi_3(x) = H_3^i(x), \quad x \in [x_{i-1},x_i]. \end{equation}

Неважко написати явний вигляд цього багаточлена $H_3^i(x)$ на проміжку:

$x_i$	$y_i$
		$y_i'$
$x_i$	$y_i$		$\frac{y_{i-1,i}-y_i'}{h_i}$
		$y_{i-1,i}$		$\frac{y_i' - 2 y_{i-1,i}+y_{i-1}'}{h_i^2}$
$x_{i-1}$	$y_{i-1}$		$\frac{y_{i-1}'-y_{i-1,i}}{h_i}$
		$y_{i-1}'$
$x_{i-1}$	$y_{i-1}$

\begin{equation} H_3^i(x) = y_i + y_i’(x-x_i) + \frac{y_{i-1,i}-y_i’}{h_i} \cdot (x-x_i)^2 + \frac{y_i’ - 2 y_{i-1,i}+y_{i-1}’}{h_i^2} \cdot (x-x_i)^2 \cdot (x-x_{i-1}) \end{equation}

Можна представити кусково-кубічну функцію і в такому вигляд:

\begin{equation} \label{eq:6.10.2} \Phi_3(x) = \Sum_{i = 0}^n (y_i \cdot \varphi_i^0 (x) + y_i’ \cdot \varphi_i^1(x)). \end{equation}

Умови інтерполювання: $\Phi_3(x_i) = y_i$, $\Phi_3'(x_i) = y_i'$, $i = \overline{0,n}$. Якщо ці умови підставити в \уйref{eq:6.10.2}, то отримаємо умови на базисні функції:

\begin{align} \varphi_i^0(x_j) &= \delta_{i,j}, \newline \left(\varphi_i^0\right)^\prime(x_j) &= 0, \newline \varphi_i^1(x_j) &= 0, \newline \left(\varphi_i^1\right)^\prime(x_j) &= \delta_{i,j}. \end{align}

для $i,j=\overline{0,n}$.

Ці функції кусково-кубічні, тобто $\varphi_i^k(x) \in \pi_3$, $x \in [x_{i - 1}, x_{i + 1}]$, $k = 0, 1$ ($\pi_3$ — множина багаточленів третього степеня), на всіх інших проміжка вони нульові. Нехай $h_i \equiv h$, і позначимо $s = \frac{x - x_i}{h}$, $x \in [x_{i - 1}, x_i] \implies s \in [-1,0]$.

1. введемо $\overline \varphi_1^0(s) = \varphi_i^0(x)$, $x \in [x_{i - 1}, x_{i + 1}]$, $x \in [0,1]$. Побудуємо цю функцію. Вона задовольняє умовам:

   \begin{align} \overline \varphi_1^0(0) &= 1, \newline \overline \varphi_1^0(1) &= 0, \newline \left(\overline \varphi_1^0\right)^\prime(0) &= 0, \newline \left(\overline \varphi_1^0\right)^\prime(1) &= 0. \end{align}

   Її явний вигляд отримаємо за допомогою таблиці розділених різниць:

   $0$	$1$
   		$0$
   $0$	$1$		$-1$
   		$-1$		$2$
   $1$	$0$		$1$
   		$0$
   $1$	$0$

   \begin{equation} H_3(s) = 1 + 0 \cdot s - 1 \cdot s^2 + 2 s^2(s-1) = 2s^3 - 3s^2 + 1 \equiv \overline \varphi_1^0(s). \end{equation}

   Аналогічно

2. $\overline \varphi_2^0(s) = -2s^3 - 3s^2 + 1$, $\varphi_i^0(x) = \overline \varphi_2^0(s)$, $x \in [x_{i - 1}, x_i]$, $s \in [-1,0]$;

3. $\overline \varphi_1^1(s) = s(s-1)^2$, $\varphi_i^0(x) = h \overline \varphi_1^1(s)$, $x \in [x_i, x_{i+1}]$, $s \in [0,1]$;

4. $\overline \varphi_2^1(s) = s(s+1)^2$, $\varphi_i^0(x) = h \overline \varphi_2^1(s)$, $x \in [x_{i-1}, x_i]$, $s\in[-1,0]$.

А тепер будуємо явний вигляд функцій $\varphi_i^k(x)$ для довільного проміжку $x\in[x_{i-1},x_{i+1}]$:

\begin{equation} \varphi_i^0(x) = \begin{cases} 0, & a \le x \le x_{i-1}, \newline -2s^3 - 3s^2 + 1, & x_{i-1} \le x \le x_i, \newline 2s^3 - 3s^2 + 1, & x_i \le x \le x_{i+1}, \newline 0, & x_{i+1} \le x \le b, \end{cases} \end{equation}

і

\begin{equation} \varphi_i^1(x) = \begin{cases} 0, & a \le x \le x_{i-1}, \newline hs(s+1)^2, & x_{i-1} \le x \le x_i, \newline hs(s-1)^2, & x_i \le x \le x_{i+1}, \newline 0, & x_{i+1} \le x \le b, \end{cases} \end{equation}

де $s = \frac{x-x_i}{h}$ (якщо сітка нерівномірна, то в формулах замість $h$, буде $h_i$ або $h_{i+1}$ на відповідних інтервалах).

Оцінимо $\| f(x) - \Phi_3(x)\|\void_{C([a, b])}$. Розглянемо для $x \in [x_{i-1}, x_i]$:

\begin{equation} f(x) - \Phi_3(x) = f(x) - H_3^i(x) = \frac{f^{(4)}(\xi)}{4!} \cdot (x - x_{i-1})^2 (x - x_i)^2. \end{equation}

Зразу потрібно зробити припущення, що $f(x) \in C^4([a,b])$. З тих же міркувань, що і для кусково-лінійної функції, максимум знаходиться в точці $\overline x_i = \frac{x_i + x_{i-1}}{2}$ тому для модуля похибки маємо:

\begin{align} |f(x) - \Phi_3(x)| &\le \frac{M_4^i}{24} \left( \frac{h^2}{4} \right)^2 = \frac{M_4^i h^4}{384}, \newline |f(x) - \Phi_3(x)|\void_{C([a,b])} &\le \frac{M_4 h^4}{384}. \end{align}

Звідси отримаємо теорему:

Теорема: Якщо функція $f(x) \in C^4([a,b])$ задана в точках $x_i$ своїми значеннями $y_i = f(x_i)$, $y_i' = f'(x_i)$, $i = \overline{0,n}$, то для кусково-кубічної ермітової інтерполяції

\begin{equation} \Phi_3(x) = \Sum_{i = 0}^n \left( y_i \varphi_i^{(0)} (x) + y_i’ \varphi_i’(x) \right) \end{equation}

має місце оцінка

\begin{equation} \left| f(x) - \Phi_3(x) \right|\void_{C([a,b])} \le \frac{M_4 h^4}{384}. \end{equation}

А для похідної

\begin{equation} \left| f’(x) - \Phi_3’(x) \right|\void_{C([a,b])} \le M \cdot M_4 h^3, \end{equation}

де $M$ — стала незалежна від $h$.

Задача 17: Довести оцінку для $\left\| f'(x) - \Phi_3'(x) \right\|\void_{C([a,b])}$.

Порівняємо кусково-лінійну $\Phi_1(x)$ та кусково-кубічну інтерполяцію $\Phi_3(x)$: при згущенні сітки у $2$ рази точність лінійної підвищується в $4$ рази, а кубічної — у $16$ разів, але треба задавати більше даних.

6.11. Кубічні інтерполяційні сплайни

Сплайн (spline) в перекладі означає рейка, якою користувалися креслярі при проведені гладкої кривої, що з’єднувала задані точки на площині.

Означення: Функція $s(x)$ називається сплайном степеня $m$ і дефекту $k$, якщо

1. $s(x) \in \pi_m$ (множина поліномів степеня $m$) для $x \in [x_{i-1}, x_i]$, $i = \overline{1,n}$.

2. $s(x) \in C^{(m - k)}([a, b])$.

Приклади:

1. $\Phi_1(x)$: $m = 1$, $k = 1$;

2. $\Phi_3(x)$: $m = 3$, $k = 2$;

Зараз ми побудуємо сплайн, для якого $m = 3$, $k = 1$.

Означення: Функція $s_3(x) = s(x)$ називається кубічним інтерполяційним природнім сплайном, якщо

1. Кубічність:

   \begin{equation} \label{eq:6.11.1} s(x) \in \pi_3, \quad x \in [x_{i-1}, x_i], \quad i = \overline{1,n} \end{equation}

2. Дефект 1:

   \begin{equation} \label{eq:6.11.2} s(x) \in C^{(2)}([a,b]) \end{equation}

3. Інтерполює $f(x)$:

   \begin{equation} \label{eq:6.11.3} s(x_i) = f(x_i), \quad i = \overline{0, n} \end{equation}

4. Природній:

   \begin{equation} \label{eq:6.11.4} s^{\prime\prime}(a) = s^{\prime\prime}(b) = 0. \end{equation}

Умови \eqref{eq:6.11.4}, так звані умови природності, необхідні, щоб разом було $4 n$ умов для знаходження $4 n$ коефіцієнтів сплайну. Замість них можуть бути такі умови:

\begin{align} & s^{\prime\prime}(a) = A, \quad s^{\prime\prime}(b) = B \tag{4.a} \newline & s’(a) = A, \quad s’(b) = B \tag{4.b} \newline & s(a) = s(b), \quad s’(a) = s’(b), \quad s^{\prime\prime}(a) = s^{\prime\prime}(b) \tag{4.c} \end{align}

Умови $(4.c)$ — це так звані умови періодичності.

Побудуємо природній сплайн. З \eqref{eq:6.11.1} та \eqref{eq:6.11.2} маємо

\begin{equation} \label{eq:6.11.5} s^{\prime\prime}(x) = m_{i-1} \cdot \frac{x_i - x}{h_i} + m_i \cdot \frac{x - x_{i - 1}}{h_i}, \end{equation}

де $m_i = s^{\prime\prime}(x_i)$ і вони є невідомими коефіцієнтами: $h_i = x_i - x_{i-1}$.

Двічі інтегруючи \eqref{eq:6.11.5}, маємо

\begin{equation} \label{eq:6.11.6} \begin{aligned} s(x) &= m_{i-1} \cdot \frac{(x_i - x)^3}{6 h_i} + m_i \cdot \frac{(x - x_{i-1})^3}{6 h_i} + \newline & \quad + \left(f_{i-1} - \frac{m_{i-1}h_i^2}{6}\right) \cdot \frac{x_i - x}{h_i} + \left(f_i -\frac{m_i h_i^2}{6}\right) \cdot \frac{x - x_{i-1}}{h_i}, \end{aligned} \end{equation}

для $x \in [x_{i-1}, x_i]$.

З \eqref{eq:6.11.4} маємо $m_0 = m_n = 0$.

Враховуючи, що $s'(x_i - 0) = s'(x_i + 0)$ отримаємо СЛАР для знаходження всіх $m_i = s^{\prime\prime}(x_i)$:

\begin{equation} \label{eq:6.11.7} \left\{ \begin{aligned} & \frac{h_i m_{i-1}}{6} + \frac{(h_i + h_{i+1}) m_i}{3} + \frac{h_{i+1} m_{i+1}}{6} = \newline & \quad = \frac{f_{i+1} - f_i}{h_i} - \frac{f_i - f_{i-1}}{h_i}, \quad i = \overline{1,n-1}, \newline & m_0 = m_n = 0. \end{aligned} \right. \end{equation}

Це тридіагональна СЛАР; її можна розв’язати методом прогонки за $Q = O(N)$ арифметичних операцій.

Задача 18: Написати СЛАР для кубічного інтерполяційного сплайну, якщо $s'(a) = A$, $s'(b) = B$ та розробити алгоритм її розв’язання (тобто написати формули методу прогонки).

Теорема: Нехай $f(x) \in C^{(4)}([a,b])$, тоді має місце оцінка

\begin{equation} \left| f^{(k)}(x) - s^{(k)}(x) \right|\void_{C([a,b])} \le M_4 |h|^{4 - k}, \end{equation}

де $k = 0, 1, 2$ і $M_4 = \Max_{[a, b]} \left\vert f^{(4)}(x) \right\vert$, $\vert h \vert = \Max_i h_i$.

Введемо клас функцій

\begin{equation} U = \left\{ u(x): u(x) \in W_2^2([a,b]) , u(x_i) = f_i, i = \overline{0,n} \right\}
\end{equation}

— це функції досить гладкі і приймають задані значення. Якщо ввести такий функціонал

\begin{equation} \Phi(u) = \Int_a^b (u^{\prime\prime}(x))^2 \diff x, \end{equation}

то

\begin{equation} \Phi(s) = \Inf_{u \in U} \Phi(u), \end{equation}

де $s(x)$ — кубічний природній інтерполяційний сплайн.

Оскільки кривизна графіка кривої $u(x)$ пропорційна $u^{\prime\prime}(x)$, то це фактично означає, що сплайн має в середньоквадратичному розумінні найменшу кривизну серед всіх функцій $u(x) \in W_2^2([a,b])$, що інтерполюють значення $f(x_i)$.

Для того, щоб не розв’язувати СЛАР $(116)$ інколи будують наближення до сплайну $\tilde s(x)$, яке отримується заміною $m_i = s^{\prime\prime}(x_i)$ на

\begin{equation} f_{\bar x, \hat x, i} \equiv \frac{1}{\bar h_i} \left( \frac{f_{i+1}-f_i}{h_{i+1}} - \frac{f_i - f_{i-1}}{h_i} \right) \approx f^{\prime\prime}(x_i) \approx s^{\prime\prime}(x_i), \end{equation}

де $\bar h_i = \frac{h_i + h_{i+1}}{2}$, причому $f^{\prime\prime}(x_i) - f_{\bar x \hat x, i} = O(\vert h\vert^2)$; При цьому і $\tilde s(x) - s(x) = O(h^4)$. Відмітимо, що $\tilde s(x)$ не є сплайном дефекту 1.

Зауваження 1: Складемо матрицю $A$ розмірності $(n - 1) \times (n - 1)$:

\begin{equation} A = \begin{pmatrix} \frac{h_1 + h_2}{3} & \frac{h_2}{6} & 0 & \ldots & 0 \newline \frac{h_2}{6} & \frac{h_2 + h_3}{3} & \frac{h_3}{6} & \ddots & \vdots \newline 0 & \frac{h_3}{6} & \frac{h_3 + h_4}{3} & \ddots & 0 \newline \vdots & \ddots & \ddots & \ddots & \ddots \newline 0 & \ldots & 0 & \frac{h_{n - 1}}{6} & \frac{h_{n-1} + h_n}{3} \end{pmatrix} \end{equation}

і матрицю $H$ розмірності $(n + 1) \times (n - 1)$:

\begin{equation} H = \begin{pmatrix} \frac{1}{h_1} & - \left(\frac{1}{h_1} + \frac{1}{h_2}\right) & \frac{1}{h_2} & 0 & \ldots & 0 \newline 0 & \frac{1}{h_2} & - \left(\frac{1}{h_2} + \frac{1}{h_3}\right) & \frac{1}{h_3} & \ddots & \vdots \newline \vdots & \ddots & \ddots & \ddots & \ddots & 0 \newline 0 & \ldots & 0 & \frac{1}{h_{n - 1}} & - \left(\frac{1}{h_{n-1}}+\frac{1}{h_n}\right) & \frac{1}{h_n} \end{pmatrix} \end{equation}

Тоді можна записати СЛАР $(116)$ відносно моментів $\vec m = (m_1, m_2, \ldots, m_{n-1})$ вигляді:

\begin{equation} A \vec m = F \vec f, \end{equation}

де

\begin{equation} \vec f = (f_0, f_1, \ldots, f_n)^\intercal \end{equation}

Зауваження 2: Нагадаємо формулу для інтерполяційного багаточлена Лагранжа

\begin{equation} L_n(x) = \Sum_{i = 0}^n f(x_i) \Phi_i^{(n)}(x), \end{equation}

де $\Phi_i^{(n)}$ — множники Лагранжа. Це представлення інтерполяційного багаточлена Лагранжа по системі функцій $\left\{\Phi_i^{(n)}\right\}$. Для

\begin{equation} \Phi_1 = \Sum_{i = 1}^n f(x_i) \varphi_i(x) \end{equation}

маємо представлення по системі кусково-лінійних функцій $\{\varphi_i(x)\}$. Для

\begin{equation} \Phi_3(x) = \Sum_{i = 1}^n \left( f(x_i) \varphi_i^0(x) + f’(x_i) \left( \varphi_i^1 \right) ‘(x) \right) \end{equation}

— представлення по системі $\left\{\varphi_i^0, \left( \varphi_i^1 \right)' \right\}$.

Аналогічно, якщо представити кубічний сплайн у вигляді

\begin{equation} s_3(x) = \Sum_{i = 0}^n c_i B_3^i(x), \end{equation}

то відповідна система для кубічного сплайну буде $\left\{ B_3^i(x) \right\}^n_{i = 1}$. Тут $B_3^i(x)$ — так званий кубічний $B_3$-сплайн. Формула дається, а графік представлено на рис.:

\begin{equation} B_3^i(z) = \frac{1}{6h} \begin{cases} \left(\frac{z - x_{i-2}}{h}\right)^3, & z \in [x_{i - 2}, x_{i - 1}]; \newline - 3 \left(\frac{z - x_{i - 1}}{h}\right)^3 + 3 \left(\frac{z - x_{i-1}}{h}\right)^2 + 3 \left(\frac{z - x_{i-1}}{h}\right) + 1, & z \in [x_{i - 1}, x_i]; \newline - 3 \left(\frac{x_{i + 1} - z}{h}\right)^3 + 3 \left(\frac{x_{i-1} - z}{h}\right)^2 + 3 \left(\frac{x_{i-1} - z}{h}\right) + 1, & z \in [x_i, x_{i + 1}]; \newline \left(\frac{x_{i+2} - z}{h}\right)^3, & z \in [x_{i + 1}, x_{i + 2}]; \newline 0, & z < x_{i - 2} \lor x_{i + 2} < z. \end{cases} \end{equation}

Задача 19: Показати, що $B_3^i$ є кубічним сплайном дефекту $1$.

Для знаходження коефіцієнтів $c_i$записується СЛАР з умов інтерполювання.

6.12. Параметричні сплайни

На практиці часто виникає задача побудови кривої по заданим точкам $(x_i, y_i)^n_{i = 1}$. В цьому випадку використовують сплайни. Якщо відповідна функція $y = f(x)$ однозначна, то сплайн будується за алгоритмом з попереднього пункту.

Окремо розглянемо випадок, коли точки $(x_i, y_i)^n_{i = 1}$ в площині $(x, y)$ розташовані у довільний спосіб:

В цьому випадку відповідна функція задається параметрично

\begin{equation} \label{eq:6.12.1} x = x(t), \quad y = y(t), \quad t \in [A, B]. \end{equation}

Для значень $x_i$, $i = \overline{1,n}$ побудуємо кубічний сплайн $s_x(t)$ такий, що $s_x(t_i) = x_i$, $i = \overline{1,n}$, а для $y_i$, $i = \overline{1, n}$ будуємо сплайн $s_y(t)$, для якого $s_y(t_i) = y_i$, $i = \overline{1,n}$.

Означення: Тоді параметрична функція

\begin{equation} \label{eq:6.12.2} (s_x(t), s_y(t), \quad t \in [A, B]. \end{equation}

називається параметричним сплайном для функції \eqref{eq:6.12.2}.

Стає питання про вибір параметру $t$. Нехай $t_i = i$, $i = \overline{1,n}$, тобто для табличних даних $(x_i, y_i)^n_{i = 1}$ параметром виступає номер точки в площині $(x, y)$. Тоді для параметричного сплайну неперервний параметр $t$ змінюється на інтервалі $t \in [1,n]$.

Побудова сплайнів $s_x(t)$ та $s_y(t)$ здійснюється за алгоритмом наведеним в попередньому пункті по значенням $f_i = x_i$, $i = \overline{1,n}$ та $f_i = y_i$, $i = \overline{1,n}$.

Розглянемо тепер побудову замкненої гладкої кривої:

Параметризуємо її як в попередньому випадку. Відмінність полягає в тому, що тепер функції $x = x(t)$ та $y = y(t)$ періодичні з періодом $T = n$, тобто

\begin{equation} \forall t: \quad x(t) = x(t + n), \quad y(t) = y(t + n). \end{equation}

Наприклад, для значень в точках маємо:

\begin{equation} \label{eq:6.12.3} x_1 = x_{n + 1}, \quad y_1 = y_{n + 1}; \qquad x_0 = x_n, \quad y_0 = y_n. \end{equation}

Побудуємо алгоритм реалізації періодичного параметричного кубічного сплайну. Як і для звичайного сплайну на інтервалі $t \in [t_i , t_{i+1}]$ маємо:

\begin{equation} \begin{aligned} s(t) &= \frac{m_{i - 1} (t_i - t)^3}{6 h_i} + \frac{m_i (t - t_{i - 1})^3}{6 h_i} + \newline & \quad + \left(f_{i - 1} - \frac{m_{i - 1} h_i^2}{6}\right) \frac{t_i - t}{h_i} + \newline & \quad + \left(f_i - \frac{m_i h_i^2}{6}\right) \frac{t - t_{i - 1}}{h_i}, \end{aligned} \end{equation}

де $s(t)$ — одна з функцій $s_x(t)$ або $s_y(t)$; $f_i = x_i$, $i = \overline{1,n}$ або $f_i = y_i$, $i = \overline{1,n}$; $h_i = t_{i+1} - t_i = 1$. Для знаходження коефіцієнтів сплайну $m_i = s''(t_i)$ з умови неперервності першої похідної сплайна маємо СЛАР:

\begin{equation} \label{eq:6.12.4} \left\{ \begin{aligned} & \frac{h_i m_{i - 1}}{6} + \frac{(h_i + h_{i + 1}) m_i}{3} + \frac{h_{i + 1} m_{i + 1}}{6} = \newline & \quad = \frac{f_{i + 1} - f_i}{h_i} -\frac{f_i - f_{i - 1}}{h_i}, \quad i = \overline{1,n}, \newline & m_0 = m_n, \quad m_1 = m_{n + 1}, \end{aligned} \right. \end{equation}

Додаткові умови на коефіцієнти $m_i$ випливають з періодичності сплайну та його других похідних.

Системі $(74)$ відповідає матриця розмірності $(n \times n)$:

\begin{equation} A = \begin{pmatrix} \frac{h_1 + h_2}{3} & \frac{h_2}{6} & 0 & \cdots & 0 & \left\langle\frac{h_1}{6}\right\rangle \newline \frac{h_2}{6} & \frac{h_2 + h_3}{3} & \frac{h_3}{6} & \ddots & & 0 \newline 0 & \frac{h_3}{6} & \frac{h_3 + h_4}{3} & \ddots & \ddots & \vdots \newline \vdots & \ddots & \ddots & \ddots & \ddots & 0 \newline 0 & & \ddots & \ddots & \ddots & \frac{h_n}{6} \newline \left\langle \frac{h_1}{6} \right\rangle & 0 & \cdots & 0 & \frac{h_n}{6} & \frac{h_n + h_1}{3} \end{pmatrix} \end{equation}

яка є майже тридіагональною: «заважають» два елементи матриці, що виділені кутовими дужками.

Для розв’язання таких систем застосовують метод циклічної прогонки.

Розглянемо алгоритм цього методу для більш загальної системи:

\begin{equation} \label{eq:6.12.5} \left\{ \begin{aligned} & a_i y_{i - 1} - c_i y_i + b_i y_{i + 1} = - f_i, \quad i = \overline{1, n}, \newline & y_0 = y_n, \quad y_{n + 1} = y_1, \quad a_1 = a_n, \quad b_{n + 1} = b_1, \end{aligned} \right. \end{equation}

Формули методу [ЛМС, стор. 391–392]:

1. $\alpha_2 = b_1 / c_1$, $\beta_2 = f_1 / c_1$, $\gamma_2 = a_1 / c_1$;

2. $z_i = c_i - a_i \alpha_i$; $\alpha_{i + 1} = b_i / z_i$; $\beta_{i + 1} = (f_i + a_i \beta_i)/z_i$; $\gamma_{i + 1} = a_i \gamma_i / z_i$, $i = \overline{2, n}$;

3. $p_{n - 1} = \beta_n$; $q_{n - 1} = \alpha_n + \gamma_n$;

4. $p_i = \alpha_{i + 1} p_{i + 1} + \beta_{i + 1}$; $q_i = \alpha_{i + 1} q_{i + 1} + \gamma_{i + 1}$, $i = \overline{n - 2, 1}$;

5. $y_n = (\beta_{n + 1} + a_{n + 1} p_1) / (1 - \alpha_{n + 1} q_1 - \gamma_{n + 1})$;

6. $y_i = p_i + y_n q_i$, $i = \overline{1, n - 1}$

Метод стійкий ($\vert \alpha_i \vert < 1$, $1 - \alpha_{n + 1} \alpha_1 - \gamma_{n + 1} \ne 0$), якщо $a_i, b_i > 0$, $c_i > b_i + a_i$. Для системи $(74)$ ці умови виконані.

Метод економний, оскільки кількість арифметичних операцій, що витрачається на його реалізацію, $Q = O(n)$.

Розглянуті в цьому пункті параметричні сплайни мають хороші апроксимативні та екстремальні властивості, тому побудовані по ним криві добре відновлюють задані як при малій, так досить великій кількості точок інтерполювання

6.13. Застосування інтерполювання

1. Складання таблиць. Нехай $r_1^i(x)$ залишковий член лінійної інтерполяції по двох сусідніх точках $x_{i-1}$, $x_i$:

   \begin{equation} r_1^i(x) = f(x) - L_1^i(x) = \frac{f’’(\xi)}{2!} \cdot (x - x_{i - 1}) (x - x_i). \end{equation}

   Тоді

   \begin{equation} \left|r_1^i(x)\right| \le \frac{M_2^i}{2} \cdot |(x - x_{i - 1}) (x - x_i)| \le \frac{M_2^i h^2}{8}, \quad x \in [x_{i - 1}, x_i]. \end{equation}

   Таким чином

   \begin{equation} \left| f(x) - L_1^i(x) \right|\void_{C([a,b])} \le \frac{M_2 h^2}{8}. \end{equation}

   Ця оцінка може бути використана при складані таблиць функцій, які при відновлення проміжних значень лінійною інтерполяцією сусідніх значень забезпечують точність $\varepsilon$.

   Для того, щоб похибка була меншою за $\varepsilon$ потрібно вибрати

   \begin{equation} h \le \sqrt{\frac{8 \varepsilon}{M_2}}. \end{equation}

   Аналогічно, для квадратичного інтерполювання маємо

   \begin{equation} \left|f(x) - L_2^i(x)\right|\void_{C([a,b])} \le \frac{M_3 h^3}{9 \sqrt{3}} < \varepsilon. \end{equation}

   Звідси

   \begin{equation} h \le \sqrt[3]{\frac{9 \sqrt{3} \varepsilon}{M_3}}. \end{equation}

2. Розв’язування рівнянь. Нехай необхідно розв’язати рівняння

   \begin{equation} \label{eq:6.13.1} f(x) = \bar y. \end{equation}

   При $\bar y = 0$ маємо рівняння $f(x) = 0$. Нехай $\bar x$ корінь рівняння \eqref{eq:6.13.1}.

   1. Обернене інтерполювання. Якщо відома обернена функція $x = x(y)$, то $\bar x = x(\bar y)$. Нехай функція $f(x)$ задана значеннями $y_i = f(x_i)$, $x_i \in [a,b]$. Побудуємо інтерполяційний багаточлен $L_n(y)$ по значеннях $\{y_i, x_i\}^n_{i = 0}$ де $y_i$ вважаються значеннями аргументу, а $x_i$ — значеннями оберненої функції. Тоді наближення до кореня є $x^\star = L_n(y)$.

      Оцінимо похибку:

      \begin{equation} \label{eq:6.13.2} \left| \bar x - x^\star \right| = \left| x(\bar y) - L_n(\bar y) \right| \le \frac{M_{n+1}}{(n + 1)!} |\omega_n(\bar y)|, \end{equation}

      де $M_{n + 1} = \Max_{y_\min \le y \le y_\max} \left\vert \frac{\diff^{n + 1}}{\diff y^{n + 1}} x(y) \right\vert$, $\vert\omega_n(y)\vert = (y - y_0) \ldots (y - y_n)$.

      Недоліком методу є складність обчислення похідних старших порядків оберненої функції.

   2. Пряме інтерполювання. Нехай знову відомі $y_i = f(x_i)$, $x_i \in [a,b]$. Тоді замість рівняння \eqref{eq:6.13.1} розв’язуємо рівняння

      \begin{equation} L_n(x^\star) = y,
      \end{equation}

      де $L_n(x)$ інтерполяційний багаточлен по значенням $\{x_i, y_i\}^n_{i = 0}$.

      Недоліками методу є необхідність розв’язування алгебраїчних рівнянь $n$-го степеня та необхідність вибирати шуканий розв’язок серед $n$ коренів багаточлена степеня $n$.

      Але позитивним є те, що функція є все таки алгебраїчною (а саме багаточленом).

      Оцінимо похибку такого способу обчислення кореня. Маємо:

      \begin{equation} f(x^\star) - L_n(x) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!} \cdot \omega_n(x). \end{equation}

      Далі $f(x^\star) - y = f(x^\star) - f(\bar x)$, звідки

      \begin{equation} |f(x^\star) - f(\bar x)| \le \frac{M_{n + 1}}{(n + 1)!} \cdot |\omega_n(x)|. \end{equation}

      Тут тепер $M_{n + 1} = \Max_{x \in [a, b]} \left\vert f^{(n + 1)}(x) \right\vert$.

      За теоремою Лагранжа $f(x^\star) -f(\bar x) = f'(\eta) (x^\star - \bar x)$.

      Припустимо, що $f'(x) \ne 0$. Це означає, що на проміжку $[a,b]$ функція $f(x)$ монотонна. Звідси

      \begin{equation} |x^\star - \bar x| \le \frac{|f(x^\star) - f(\bar x)}{\Min_{x \in [a,b]} |f’(x)|} \le \frac{M_{n + 1}}{\Min_{x \in [a, b]} |f’(x)|} \cdot \frac{|\omega_n(x)|}{(n + 1)!}. \end{equation}

3. Метод інтерполювання побудови характеристичного багаточлена.

   Одним з найпростіших методів побудови характеристичного багаточлена є наступний. Відомо, що багаточлен $n$-го степеня однозначно визначається своїми значеннями в $(n + 1)$-й точці. Тому для побудови $P_n(\lambda) = \det(A - \lambda E)$ виберемо на проміжку де знаходяться власні значення (наприклад, $\lambda \in [- \|A\|\void_k, \|A\|\void_k]$, де $k = 1$ або $k = \infty$) деякі точки $\lambda_i$, $i = \overline{0,n}$. За допомогою методу Гауса для несиметричних матриць або методу квадратних коренів для симетричних матриць обчислимо $P_n(\lambda_i) = \det(A - \lambda_i E)$ і по цих значення за формулою, наприклад, Ньютона побудуємо інтерполяційний багаточлен, який співпадатиме з характеристичним.

   Далі розв’язується рівняння $P_n(\lambda) = 0$ одним з відомих методів для нелінійного рівняння. Характерно, що часто для цього використовують метод парабол (обернене інтерполювання по трьох точках, або заміна рівняння $n$-го степеня в околі кореня на квадратне рівняння за допомогою інтерполяційного багаточлена другого степеня).

   Зауважимо, що знаходження власних значень за допомогою характеристичного багаточлена пов’язана з проблемою нестійкості коренів характеристичного багаточлена відносно похибок обчислення коефіцієнтів цього багаточлена. Тому застосовують цей метод для невеликих розмірностях $n \le 10$ матриці $A$.

6.14. Тригонометрична інтерполяція

Інтерполяція відбувається за системою функцій

\begin{equation} \label{eq:6.14.1} 1, \sin (x), \cos(x), \sin(2x), \cos(2x), \ldots, \sin(kx), \cos(kx), \ldots \end{equation}

що є відрізком тригонометричного ряду Фур’є. Щоб знайти $T_n(x)$ потрібно визначити $2 n + 1$ коефіцієнт, а значить задати $(2 n + 1)$ значень періодичної з періодом $2 \pi$ функції $y_i = f_i(x)$, $i = \overline{0, 2 n}$.

Покажемо, що

\begin{equation} \label{eq:6.14.2} T_n(x) = \Sum_{i = 0}^{2n} f(x_i) \Phi_i(x), \end{equation}

де

\begin{equation} \Phi_i(x) = \Prod_{\substack{j = 0 \\ j \ne i}}^{2 n} \frac{\sin \left(\frac{x - x_j}{2}\right)}{\sin \left(\frac{x_i - x_j}{2}\right)}, \end{equation}

тобто $T_n(x_k) = f(x_k)$, та $\Phi_i(x_k) = \delta_{ik}$. Дійсно

\begin{equation} \Phi_i(x_k) = \Prod_{\substack{j = 0 \\ j \ne i}}^{2 n} \frac{\sin \left(\frac{x_k - x_j}{2}\right)}{\sin \left(\frac{x_i - x_j}{2}\right)}, \end{equation}

для $i \ne k$, а

\begin{equation} \Phi_i(x_i) = \Prod_{\substack{j = 0 \\ j \ne i}}^{2 n} \frac{\sin \left(\frac{x_i - x_j}{2}\right)}{\sin \left(\frac{x_i - x_j}{2}\right)} = 1. \end{equation}

Таким чином за допомогою формули \eqref{eq:6.14.2} ми уникли необхідності підраховувати коефіцієнти Фур’є $a_k$, $b_k$.

Нехай функція $f(x)$ є парною та неперервною на проміжку $[-\pi, \pi]$. Тоді по значенням в $(n + 1)$-й точці, $y_i = f_i(x)$, $i = \overline{0,n}$, $x_i \in [0, \pi]$ можна побудувати парний тригонометричний багаточлен:

\begin{equation} \label{eq:6.14.3} T_n(x) = \Sum_{i = 0}^{n} f(x_i) \Prod_{\substack{j = 0 \\ j \ne i}}^n \frac{\cos(x) - \cos(x_i)}{\cos(x_i) - \cos(x_j)}. \end{equation}

Якщо ж функція є непарною на проміжку $[-\pi, \pi]$, то по значенням в $n$ точках $y_i = f_i(x)$, $i = \overline{1,n}$. $x_i \in [0, \pi]$ можна побудувати непарний інтерполяційний багаточлен:

\begin{equation} \label{eq:6.14.4} T_n(x) = \Sum_{i = 1}^{n} f(x_i) \frac{\sin(x)}{\sin(x_i)} \Prod_{\substack{j = 1 \\ j \ne i}} \frac{\cos(x) - \cos(x_i)}{\cos(x_i) - \cos(x_j)}. \end{equation}

Задача 20: Показати, що тригонометричні багаточлени \eqref{eq:6.14.3}, \eqref{eq:6.14.4} є інтерполюючими для функції $f(x)$. Яке значення функції інтерполює \eqref{eq:6.14.4} при $x = 0$? Чому?

6.15. Двовимірна інтерполяція

Побудова багаточлена для функції від двох змінних $z = f(x, y)$, що інтерполює значення $z_i = f(x_i, y_i)$ в точках $A_i(x_i, y_i)$, пов’язана з такими труднощами

1. Якщо в одновимірному випадку кількість вузлів та степінь багаточлена пов’язані простою залежністю: $n + 1$ точка $x_i$ дозволяють побудувати багаточлен $n$-го степеня $L_n(x)$, то в двовимірному випадку багаточлен $n$-го степеня від двох змінних

   \begin{equation} P_n(x, y) = \Sum_{0 \le k + m \le n} a_{k,m} x^k y^m, \end{equation}

   має $N = \frac{(n + 1) (n + 2)}{2}$ коефіцієнтів $a_{k,m}$. Тому необхідно задати значення в точках $A_i(x_i, y_i)^N_{i = 1}$.

2. Не всяке розташування вузлів допустиме. Якщо розглянути умови інтерполювання

\begin{equation} P_n(x_i, y_i) = \Sum_{0 \le k + m \le n} a_{k,m} x_i^k y_i^m = z_i, \end{equation}

то для розв’язності цієї СЛАР необхідно виконання умови $\det B \ne 0$, де матриця $B$ має коефіцієнти:

\begin{equation}

\end{equation}

Ця умова, наприклад, для лінійної інтерполяції $n = 1$ та $N = 3$ вимагає, щоб вузли $A_i(x_i, y_i)$ не лежали на одній прямій. Якщо $n = 2$, то $N = 6$ і необхідно розглядати точки, які не лежать на деякій кривій другого порядку і т. д.

Розглянемо випадки, коли можна записати багаточлен для двовимірної інтерполяції в явному вигляді.

Нехай область, в якій інтерполюється функція є прямокутником:

\begin{equation} \overline \Omega = { (x, y): 0 \le x \le L_1, 0 \le y \le L_2 }. \end{equation}

Введемо сітку

\begin{equation} x_i = i h_x, \quad, h_x = L_1 / N, \quad i = \overline{0, N}; \qquad y_j = j h_y, \quad, h_y = L_2 / M, \quad j = \overline{0, M} \end{equation}

Тоді інтерполяційний багаточлен має вигляд

\begin{equation} \label{eq:6.15.1} P(x, y) = \Sum_{i = 0}^{N} \Sum_{j = 0}^{M} f(x_i, y_j) \Prod_{\substack{p = 0 \\ p \ne i}}^{N} \Prod_{\substack{q = 0 \\ q \ne j}}^{M} \left(\frac{x - x_i}{x_p - x_i} \cdot \frac{y - y_j}{y_q - y_j}\right) \end{equation}

Розглянемо випадок, коли $N = M = 1$. Тоді

\begin{equation} \label{eq:6.15.2} \begin{aligned} P_{1,1}(x, y) &= f(x_0, y_0) \cdot \frac{x - x_1}{x_0 - x_1} \cdot \frac{y - y_1}{y_0 - y_1} + f(x_0, y_1) \cdot \frac{x - x_1}{x_0 - x_1} \cdot \frac{y - y_0}{y_1 - y_0} + \newline & \quad + f(x_1, y_0) \cdot \frac{x - x_0}{x_1 - x_0} \cdot \frac{y - y_1}{y_0 - y_1} + f(x_1, y_1) \cdot \frac{x - x_0}{x_1 - x_0} \cdot \frac{y - y_0}{y_1 - y_0} = \newline &= a_0 + a_1 x + a_2 y + a_{1,2} x y. \end{aligned} \end{equation}

Це так звана білінійна інтерполяція, тобто лінійна по кожній окремій змінній.

Формула \eqref{eq:6.15.1} являє собою приклад інтерполювання на всій області. В одновимірному випадку при великих степенях багаточлена отримують погане наближення через розбіжність процесу інтерполювання. Так ж картина має місце і в двовимірному випадку. Тому найчастіше застосовують кусково-поліноміальну апроксимацію.

Коротко наведемо деякі відомості про кусково-поліноміальне інтерполювання з теорії методу скінчених елементів розв’язання крайових задач для диференціальних рівнянь в частинних похідних.

Нехай область $\Omega \subset \RR^2$ — багатокутник в площині. Представимо її у вигляді

\begin{equation} \Omega = \bigsqcup_{i = 1}^n K_i, \end{equation}

де $K_i \in T_h$.

Означення: $T_h$ називається «тріангуляцією» області $Omega$,

а $K_i$ — багатокутники з непорожньою внутрішністю що не мають спільних внутрішніх точок, причому $\diam K_i \le h$, де $h$ — характеристика щільності розбиття.

Найчастіше $K_i$ це трикутники або прямокутники.

Нехай $v \in X$ — функція, яку ми будемо інтерполювати. Позначимо $X_h$ простір, що апроксимує $X$, а його елементи $c_h \in X_h$. Причому звуження цієї функції на область $K_i$, тобто $v_h \vert_{K_i}$ є поліномом.

Позначимо $\Pi_k$, $k \ge 0$ — простір багаточленів степеня $k$ по сукупності змінних $x$, $y$; його розмірність $\dim \Pi_k = \frac{(k + 1) (k + 2)}{2}$. Нехай $\Theta_k$, $k \ge 0$ — простір багаточленів степеня по кожній окремій змінний $x$, $y$; його розмірність $\dim \Theta_k = (k + 1)^2$.

Наприклад, $P_1(x, y) = a_0 + a_1 x + a_2 y \in \Pi_1$ — поліном степеня $1$ по $x$, $y$, а $Q_1(x, y) = a_0 + a_1 x + a_2 y + a_{1,2} x y \in \Theta_1$ лінійна по кожній окремій змінній.

Позначимо через $X_h^k = \{ v_h \in C^0(\Omega): v_h \vert_k, \forall k \in T_k\}$ — простір інтерполянтів при розбитті області на трикутники, а $Y_h^k = \{v_h \in C^0(\Omega): v_h \vert_k \in \Theta_k, \forall k \in T_h\}$ — при розбитті на прямокутники.

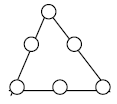
Приклад 1: Утворимо $X_h^1$, $k = 1$.

Будуємо багаточлен $1$-го степеня по двох змінних. Оскільки $\dim \Pi_1 = 3$, то для цього треба задати значення функції в трьох точках. Точки, які задано — $A_i$, i = \overline{1,3}$$ вибираємо вершинами трикутника, як на малюнку:

Тоді поліном першого степеня $z = P_1(x, y)$ є розв’язком такого рівняння відносно $z$:

\begin{equation} \begin{vmatrix} 1 & x & y & z \newline 1 & x_1 & y_1 & z_1 \newline 1 & x_2 & y_2 & z_2 \newline 1 & x_3 & y_3 & z_3 \end{vmatrix} = 0. \end{equation}

Тут $f_i = f(x_i, y_i)$, $i = \overline{1, 3}$.

Задача 21: Знайти явний вигляд $z = P_1(x, y)$ — інтерполяційного багаточлена по значенням в точках $A_i = (x_i, y_i)$, $i = 1, 2, 3$.

Приклад 2: Для $X_h^2$, $k = 2$, $\dim \Pi_2 = 6$.

Треба задати $6$ значень, щоб забезпечити однозначність наближення. Тому вибираємо точки інтерполювання так:

Приклад 3: $X_h^2$, $k = 3$, $\dim \Pi_3 = 10$.

Потрібно задати 10 точок, як на наступному малюнку:

Приклад 4: $Y_h^1$, $k = 1$, $\dim \Theta_1 = 4$.

Формула для $Q_1(x,y)$ наведена в \eqref{eq:6.15.2}. Точки:

Приклад 5: $Y_h^2$, $k = 2$, $\dim \Theta_2 = 9$.

Приклад 6: $Y_h^3$, $k = 3$, $\dim \Theta_4 = 16$.

Нехай $X = W_2^m(\Omega) = H^m(\Omega)$ — це простір з нормою

$$\begin{equation} \left\|v\right\|^2_m = \Sum_{k = 0}^{m} \left\|v_k\right\|^2, \end{equation}$$

де

\begin{equation} |v_k|^2 = \Int_\Omega (D^m v)^2 \diff \Omega = \Int_\Omega \left( \left(D_{x^k}^k x\right)^2 + \left(D_{x^{k - 1} y}^k x\right)^2 + \ldots + \left(D_{y^k}^k x\right)^2 \right) \diff \Omega \end{equation}

\begin{equation} D_{x^k}^k v = \frac{\partial^k v}{\partial x^k}; \quad D_{x^{k - 1} y}^k v = \frac{\partial^k v}{\partial x^{k - 1} \partial y}; \quad \ldots \end{equation}

Якщо $\|v\|\void_m \le M < \infty$, то $v \in W_2^m(\Omega)$, класу функцій інтегрованих з квадратом до $m$-ї похідної.

Розглянемо розбиття на трикутники. Накладемо обмеження на них.

Означення: Розбиття $T_h$ називається регулярним, якщо $\exists \sigma \ge 1$ таке, що

\begin{equation} \Max_{k \in T_h} \frac{h_k}{\rho_k} \le \sigma, \quad h_k = \diam K, \quad S \subset K, \quad \rho_k = \mu(S): \end{equation}

Якщо $h_k / \rho_k \gg 1$, то $K$ вироджується в пряму і це погано.

Теорема: Нехай $v \in W_2^{l + 1} (\Omega)$, $1 \le l \le k$, $T_h$ — регулярна тріангуляція $v_h \in X_h = \{v_h: v_h \vert_k = P_k\}$. Тоді

\begin{equation} |v - v_h|\void_m \le C h^{l + 1 - m} |v|\void_{l + 1}, \quad m = 0, 1, \quad k \ge 1. \end{equation}

Наприклад: для $k = 1$, $m = 0$: $l = 1$, $\|v - v_h\|\void_{L_2(\Omega)} = \|v - v_h\|\void_0 \le C h^2 \vert v \vert_2$. Якщо ж $k = 3$, $l = 3$, то $\| v- v_j\|\void_0 \le h^4 \vert v\vert_4$.

Ця теорема дозволяє стверджувати збіжність процесу інтерполювання. І чим більше степінь полінома на кожному елементі тим вища швидкість збіжності.

Узагальнимо результат теореми на область з гладкою границею:

Для цього вибираємо точки на границі і будуємо вписаний багатогранник. Його тріангулюємо. Далі на кожному трикутнику будуємо інтерполянт. В результаті отримуємо $v_h \in X_h^k$.

Тоді для $k = 1$, $l = 1$: $\|v - v_h\|\void_0 \le c h^{3/2} \vert v \vert\void_2$.