2. Методи розв’язання нелінійних рівнянь

Постановка задачі. Нехай маємо рівняння $f(x) = 0$, $\bar x$ — його розв’язок, тобто $f(\bar x) = 0$.

Задача розв’язання цього рівняння розпадається на етапи:

• Існування та кількість коренів.

• Відділення коренів, тобто розбиття числової вісі на інтервали, де знаходиться один корінь.

• Обчислення кореня із заданою точністю $\varepsilon$.

Для розв’язання перших двох задач використовуються методи математичного аналізу та алгебри, а також графічний метод. Далі розглядаються методи розв’язання третього етапу.

2.1. Метод ділення навпіл

Припустимо на $[a, b]$ знаходиться лише один корінь рівняння

\begin{equation} \label{eq:2.1.1} f(x) = 0 \end{equation}

для $f(x) \in C[a, b]$, який необхідно визначити. Нехай $f(a) \cdot f(b) < 0$.

Припустимо, що $f(a) > 0$, $f(b) < 0$. Покладемо $x_1 = \frac{a + b}{2}$ і підрахуємо $f(x_1)$. Якщо $f(x_1) < 0$, тоді шуканий корінь $\bar x$ знаходиться на інтервалі $(a, x_1)$. Якщо ж $f(x_1) > 0$, то $\bar x \in (x_1, b)$. Далі з двох інтервалів $(a, x_1)$ і $(x_1, b)$ вибираємо той, на границях якого функція $f(x)$ має різні знаки, знаходимо точку $x_2$ — середину вибраного інтервалу, підраховуємо $f(x_2)$ і повторюємо вказаний процес.

В результаті отримаємо послідовність інтервалів, що містять шуканий корінь $\bar x$, причому довжина кожного послідуючого інтервалу вдвічі менше попереднього.

Цей процес продовжується до тих пір, поки довжина отриманого інтервалу $(a_n, b_n)$ не стане меншою за $b_n - a_n < 2 \varepsilon$. Тоді $x_{n + 1}$, як середина інтервалу $(a_n, b_n)$, пов’язане з $\bar x$ нерівністю

\begin{equation} \label{eq:2.1.2} \vert x_{n + 1} - \bar x \vert < \varepsilon. \end{equation}

Ця умова для деякого $n$ буде виконуватись за теоремою Больцано-Коші. Оскільки

\begin{equation} \vert b_{k + 1} - a_{k + 1} = \frac{\vert b_k - a_k \vert}{2}, \end{equation}

то

\begin{equation} \vert x_{n + 1} - \bar x \vert \le \frac{b - a}{2^{n + 1}} < \varepsilon. \end{equation}

Звідси отримаємо нерівність для обчислення кількості ітерацій $n$ для виконання умови \eqref{eq:2.1.2}:

\begin{equation} n = n(\varepsilon) \ge \left[ \log \left( \frac{b - a}{\varepsilon} \right) \right] + 1. \end{equation}

Степінь збіжності — лінійна, тобто геометричної прогресії з знаменником $q = 1/2$.

• Переваги методу: простота, надійність.

• Недоліки методу: низька швидкість збіжності; метод не узагальнюється на системи.

2.2. Метод простої ітерації

Спочатку рівняння

\begin{equation} \label{eq:2.2.1} f(x) = 0 \end{equation}

замінюється еквівалентним

\begin{equation} \label{eq:2.2.2} x = \varphi(x). \end{equation}

Ітераційний процес має вигляд

\begin{equation} \label{eq:2.2.3} x_{n + 1} = \varphi(x_n), \quad n = 0, 1, \ldots \end{equation}

Початкове наближення $x_0$ задається.

Для збіжності велике значення має вибір функції $\varphi(x)$. Перший спосіб заміни рівняння полягає в відділенні змінної з якогось члена рівняння. Більш продуктивним є перехід від рівняння \eqref{eq:2.2.1} до \eqref{eq:2.2.2} з функцією $\varphi(x) = x + \tau(x) \cdot f(x)$, де $\tau(x)$ — знакостала функція на тому відрізку, де шукаємо корінь.

Означення: Кажуть, що ітераційний метод збігається, якщо $\Lim_{k \to \infty} x_k = \bar x$.

Далі $U_r = \left\{x : \vert x - a \vert \le r\right\}$ відрізок довжини $2 r$ з серединою в точці $a$.

З’ясуємо умови, при яких збігається метод простої ітерації.

Теорема 1: Якщо

\begin{equation} \Max_{x \in [a, b] = U_r} \vert \varphi’(x) \vert \le q < 1 \end{equation}

то метод простої ітерації збігається і має місце оцінка

\begin{equation} \label{eq:2.2.4} \vert x_n - \bar x \vert \le \frac{q_n}{1 - q} \cdot \vert x_0 - x_1 \vert \le \frac{q^n}{1 - q} \cdot (b - a). \end{equation}

Доведення: Нехай $x_{k + 1}, x_k \in U_r$. Тоді

\begin{equation} \begin{aligned} \vert x_k - x_{k - 1} \vert &= \vert \varphi(x_k) - \varphi(x_{k - 1}) \vert = \vert \varphi’(\xi_k) \cdot (x_k - x_{k - 1}) \vert \le \vert \varphi’(\xi_k) \vert \cdot \vert x_k - x_{k - 1} \vert \le \newline &\le q \cdot \vert x_k - x_{k - 1} \vert = \ldots = q^k \cdot \vert x_1 - x_0 \vert, \end{aligned} \end{equation}

де $\xi_k = x_k + \theta_k \cdot (x_{k + 1} - x_k)$, а у свою чергу $0 < \theta_k < 1$. Далі

\begin{align} \vert x_{k + p} - x_k \vert &= \vert x_{k + p} - x_{k + p - 1} + \ldots + x_{k + 1} - x_k \vert = \vert x_{k + p} - x_{k + p - 1} \vert + \ldots + \vert x_{k + 1} - x_k \vert \le \nonumber \newline &\le \left( q^{k + p - 1} + q^{k + p - 2} + \ldots + q^k \right) \cdot \vert x_1 - x_0 \vert = \frac{q^k - q^{k + p - 1}}{1 - q} \cdot \vert x_1 - x_0 \vert \xrightarrow[k \to \infty]{} 0. \label{eq:2.2.5} \end{align}

Бачимо що $\{x_k\}$ — фундаментальна послідовність. Значить вона збіжна. При $p \to \infty$ в \eqref{eq:2.2.5} отримуємо \eqref{eq:2.2.4}. $\square$

Визначимо кількість ітерацій для досягнення точності $\varepsilon$. З оцінки в теоремі $1$ отримаємо

\begin{equation} \vert x_n - \bar x \vert \le \frac{q^n}{1 - q} \cdot (b - a) < \varepsilon, \end{equation}

звідки безпосередньо маємо

\begin{equation} n(\varepsilon) = n \ge \left[ \frac{\ln \left( \frac{\varepsilon (1 - q)}{b - a} \right)}{\ln q} \right] + 1. \end{equation}

Практично ітераційний процес зупиняємо при: $\vert x_n - x_{n - 1} \vert < \varepsilon$. Але ця умова не завжди гарантує, що $\vert x_n - \bar x \vert < \varepsilon$.

Зауваження: Умова збіжності методу може бути замінена на умову Ліпшиця

\begin{equation} \vert \varphi(x) - \varphi(y) \vert \le q \cdot \vert x - y \vert, \quad 0 < q < 1. \end{equation}

• Переваги методу: простота; при $q < 1/2$ — швидше збігається ніж метод ділення навпіл; метод узагальнюється на системи.

• Недоліки методу: при $q > 1/2$ збігається повільніше ніж метод ділення навпіл; виникають труднощі при зведенні $f(x) = 0$ до $x = \varphi(x)$.

2.3. Метод релаксації

Якщо в методі простої ітерації для рівняння $x = x + \tau \cdot f(x) \equiv \varphi(x)$ вибрати $\tau(x) = \tau = \text{const}$, то ітераційний процес приймає вигляд

\begin{equation} \label{eq:2.3.1} x_{n + 1} = x_n + \tau \cdot f(x_n), \end{equation}

де $k = 0, 1, 2, 3 \ldots$, а $x_0$ — задано. Метод можна записати у вигляді

\begin{equation} \frac{x_{k + 1} - x_k}{\tau} = f(x_k), \quad k = 0, 1, \ldots \end{equation}

Оскільки $\varphi'(x) = 1 + \tau \cdot f'(x)$, то метод збігається при умові

\begin{equation} \vert \varphi’(x) \vert = \vert 1 + \tau \cdot f’(x) \vert \le q < 1. \end{equation}

Нехай $f'(x) < 0$, тоді \eqref{eq:2.2.3} запишеться у вигляді: $-q \le 1 + \tau \cdot f'(x) \le q < 1$. Звідси

\begin{equation} f’(x) \le 1 + q < 2 k \tau, \end{equation}

і

\begin{equation} 0 < \tau < \frac{2}{\vert f’(x)\vert}. \end{equation}

Поставимо задачу знаходження $\tau$, для якого $q = q(\tau) \to \min$. Для того, щоб вибрати оптимальний параметр $\tau$, розглянемо рівняння для похибки $z_k = x_k - \bar x$.

Підставивши $x_k = x + z_k$ в \eqref{eq:2.3.1}, отримаємо

\begin{equation} z_{k + 1} = z_k + \tau \cdot f(x + z_k). \end{equation}

В припущені $f(x) \in C^1([a,b])$ з теореми про середнє маємо

\begin{equation} f (\bar x + z_k) = f(\bar x) + z_k \cdot f’(\bar x + \theta \cdot z_k) = z_k \cdot f’(\bar x + \theta \cdot z_k) = z_k \cdot f’(\xi_k), \end{equation}

тобто

\begin{equation} z_{k + 1} = z_k + \tau \cdot f’(\xi_k) \cdot z_k. \end{equation}

Звідси

\begin{equation} \vert z_{k + 1} \vert \le \vert 1 + \tau \cdot f’(\xi_k) \vert \cdot \vert z_k \vert \le \Max_U \vert 1 + \tau \cdot f’(\xi_k) \vert \cdot \vert z_k \vert. \end{equation}

А тому

\begin{equation} \vert z_{k + 1} \vert \le \max \left\{ \vert 1 - \tau M_1 \vert, \vert 1 - \tau m_1 \vert \right\} \cdot \vert z_k \vert, \end{equation}

де

\begin{equation} m_1 = \Min_{[a, b]} \vert f’(x) \vert, \quad M_1 = \Max_{[a, b]} \vert f’(x) \vert \end{equation}

Таким чином, задача вибору оптимального параметра зводиться до знаходження $\tau$, для якого функція

\begin{equation} q(\tau) = \max \left\{ \vert 1 - \tau M_1 \vert, \vert 1 - \tau m_1 \vert \right\} \end{equation}

приймає мінімальне значення: $q(\tau) \to \min$.

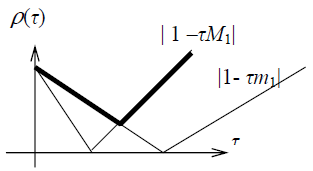
З графіка видно, що точка мінімуму визначається умовою $\vert 1 - \tau M_1 \vert = \vert 1 - \tau m_1 \vert$. Тому

\begin{equation} 1 - \tau_0 m_1 = \tau_0 M_1 - 1 \implies \tau_0 = \frac{2}{M_1 - m_1} < \frac{2}{\vert f’(x) \vert}. \end{equation}

При цьому значенні $\tau$ маємо

\begin{equation} q(\tau_0) = \rho_0 = \frac{M_1 - m_1}{M_1 + m_1}. \end{equation}

Тоді для похибки вірна оцінка

\begin{equation} \vert x_n - \bar x \vert \le \frac{\rho_0^n}{1 - \rho_0} \cdot (b - a) < \varepsilon. \end{equation}

Кількість ітерацій

\begin{equation} n = n(\varepsilon) \ge \left[ \frac{\frac{\ln (\varepsilon (1 - \rho_0))}{b - a}}{\ln \rho_0} \right] + 1. \end{equation}

Задача 1: Дати геометричну інтерпретацію методу простої ітерації для випадків:

\begin{equation} 0 < \varphi’(x) < 1; \quad -1 < \varphi’(x) < 0; \quad \varphi’(x) < -1; \quad \varphi’(x) > 1. \end{equation}

Задача 2: Знайти оптимальне $\tau = \tau_0$ для методу релаксації при $f'(x) > 0$.

2.4. Метод Ньютона (метод дотичних)

Припустимо, що рівняння $f(x) = 0$ має простий дійсний корінь $\bar x$, тобто $f(\bar x) = 0$, $f'(x) \ne 0$. Нехай виконуються умови: $f(x) \in C^1([a,b])$, $f(a) \cdot f (b) < 0$. Тоді

\begin{equation} 0 = f(\bar x) = f(x_k + \bar x - x_k) = f(x_k) + f’(\xi_k) \cdot (x - x_k), \end{equation}

де $\xi_k = x_k + \theta_k \cdot (\bar x - x_k)$, $0 < \theta_k < 1$, $\xi_k \approx x_k$. Тому наступне наближення виберемо з рівняння

\begin{equation} f(x_k) + f’(x_k) \cdot (x_{k + 1} - x_k) = 0. \end{equation}

Звідси маємо ітераційний процес

\begin{equation} x_{k + 1} = x_k - \frac{f(x_k)}{f’(x_k)}, \end{equation}

де $k = 0, 1, 2, \ldots$; $x_0$ — задане.

Метод Ньютона ще називають методом лінеаризації або методом дотичних.

Задача 3: Дати геометричну інтерпретацію методу Ньютона.

Метод Ньютона можна інтерпретувати як метод простої ітерації з

\begin{equation} \varphi(x) = x - \frac{f(x)}{f’(x)}, \end{equation}

тобто

\begin{equation} \tau(x) = - \frac{1}{f’(x)}. \end{equation}

Тому

\begin{equation} \varphi’(x) = 1 - \frac{f’(x) \cdot f’(x) - f(x) \cdot f^{\prime\prime}(x)}{(f’(x))^2} = \frac{f(x) \cdot f^{\prime\prime}(x)}{(f’(x))^2}. \end{equation}

Якщо $\bar x$ — корінь $f(x)$, то $\varphi'(x) = 1$. знайдеться окіл кореня, \end{equation}

\begin{equation} \vert \varphi’(x) \vert = \left\vert \frac{f(x) \cdot f^{\prime\prime}(x)}{(f’(x))^2} \right\vert < 1. \end{equation}

Це означає, що збіжність методу Ньютона залежить від вибору $x_0$.

Недолік методу Ньютона: необхідність обчислювати на кожній ітерації не тільки значення функції, а й похідної.

Модифікований метод Ньютона позбавлений цього недоліку і має вигляд:

\begin{equation} x_{k + 1} = x_k - \frac{f(x_k)}{f’(x_0)}, \quad k = 0, 1, 2, \ldots \end{equation}

Цей метод має лише лінійну збіжність: $\vert x_{k + 1} - x = O(\vert x_k - \bar x \vert)$.

Задача 4: Дати геометричну інтерпретацію модифікованого методу Ньютона.

В методі Ньютона, для якого $f'(x_k)$ замінюється на

\begin{equation} \frac{f(x_k) - f(x_{k - 1})}{x_k - x_{k - 1}} \end{equation}

дає метод січних:

\begin{equation} x_{k + 1} = x_k - \frac{x_k - x_{k - 1}}{f(x_k) - f(x_{k - 1})} \cdot f(x_k), \end{equation}

де $k = 1, 2, \ldots$, $x_0, x_1$ — задані.

Задача 5: Дати геометричну інтерпретацію методу січних.

2.5. Збіжність методу Ньютона

Теорема 1: Нехай $f(x) \in C^2([a,b])$; $\bar x$ простий дійсний корінь рівняння

\begin{equation} \label{eq:2.5.1} f(x) = 0. \end{equation}

і $f'(x) \ne 0$ при $x \in U_r = \left\{ x : \vert x - \bar x \vert < r \right\}$. Якщо

\begin{equation} \label{eq:2.5.2} q = \frac{M_2 \cdot \vert x_0 - \bar x \vert}{2 m_1} < 1, \end{equation}

де

\begin{equation} m_1 = \Min_{U_r} \vert f’(x) \vert, \quad M_2 = \Max_{U_r} \vert f^{\prime\prime}(x) \vert, \end{equation}

то для $x_0 \in U_r$ метод Ньютона

\begin{equation} \label{eq:2.5.3} x_{k + 1} = x_k - \frac{f(x_k)}{f’(x_k)} \end{equation}

збігається і має місце оцінка

\begin{equation} \label{eq:2.5.4} \vert x_n - \bar x \vert \le q^{2^n - 1} \cdot \vert x_0 - \bar x \vert. \end{equation}

З \eqref{eq:2.5.3} маємо

\begin{equation} \label{eq:2.5.5} x_{k + 1} - \bar x = x_k - \frac{f(x_k)}{f’(x_k)} - \bar x = \frac{(x_k - \bar x) \cdot f’(x_k) - f(x_k)}{f’(x_k)} = \frac{F(x_k)}{f’(x_k)}, \end{equation}

де $F(x) = (x - \bar x) f'(x) - f(x)$, така, що

• $F(\bar x) = 0$;

• $F'(x) = (x - \bar x) \cdot f^{\prime\prime}(x)$.

Тоді

\begin{equation} F(x_k) = F(\bar x) + \Int_x^{x_k} F’(t) \diff t = \Int_x^{x_k} (t - \bar x) \cdot f^{\prime\prime}(t) \diff t. \end{equation}

Так як $(t - \bar x)$ не міняє знак на відрізку інтегрування, то скористаємося теоремою про середнє значення:

\begin{equation} \label{eq:2.5.6} F(x_k) = f^{\prime\prime}(\xi_k) \Int_x^{x_k} (t - \bar x) \diff t = \frac{(x_k - x)^2}{2} \cdot f^{\prime\prime}(\xi_k), \end{equation}

де $\xi_k = \bar x + \theta_k \cdot (x_k - \bar x)$, де $0 < \theta_k < 1$. З \eqref{eq:2.5.5}, \eqref{eq:2.5.6} маємо

\begin{equation} \label{eq:2.5.7} x_{k + 1} - \bar x = \frac{(x_k - \bar x)^2}{2 f’(x_k)} \cdot f^{\prime\prime}(\xi_k). \end{equation}

Доведемо оцінку \eqref{eq:2.5.3} за індукцією. Так як $x_0 \in U_r$, то

\begin{equation} \vert \xi_0 - \bar x \vert = \vert \theta_0 \cdot (x_0 - \bar x) \vert < \vert \theta_0 \vert \cdot \vert x_0 - \bar x \vert < r \end{equation}

звідси випливає $\xi_0 \in U_r$.

Тоді $f^{\prime\prime}(\xi_0) \le M_2$, тому

\begin{equation} \vert x_1 - \bar x \vert \le \frac{(x_0 - \bar x)^2 \cdot M_2}{2 m_1} = \frac{M_2 \cdot \vert x_0 - \bar x \vert}{2 m_1} \cdot \vert x_0 - \bar x \vert = q \cdot \vert x_0 - \bar x \vert < r, \end{equation}

тобто $x_1 \in U_r$.

Ми довели твердження \eqref{eq:2.5.4} при $n = 1$. Нехай воно справджується при $n = k$

\begin{align} \vert x_k - \bar x \vert &\le q^{2^k - 1} \cdot \vert x_0 - \bar x \vert < r, \newline \vert \xi_k - \bar x \vert &= \vert \theta_k \cdot (x_k - \bar x) \vert < r. \end{align}

Тоді $x_k, \xi_k \in U_r$.

Доведемо \eqref{eq:2.5.4} для $n = k + 1$. З \eqref{eq:2.5.7} маємо

\begin{equation} \begin{aligned} \vert x_{k + 1} - \bar x \vert &\le \frac{\vert x_k - \bar x \vert^2 \cdot M_2}{2 m_1} \le \left( q^{2^k - 1} \right)^2 \cdot \frac{\vert x_0 - \bar x \vert^2 \cdot M_2}{2 m_1} = \newline &= q^{2^{k + 1} - 2} \cdot \frac{\vert x_0 - \bar x \vert \cdot M_2}{2 m_1} \cdot \vert x_0 - \bar x \vert = q^{2^{k + 1} - 1} \cdot \vert x_0 - \bar x \vert. \end{aligned} \end{equation}

Таким чином \eqref{eq:2.5.4} справджується для $n = k + 1$. Значить \eqref{eq:2.5.4} виконується і для довільного $n$. Таким чином $x_n \xrightarrow[n \to \infty]{} x$. $\square$

З \eqref{eq:2.5.4} маємо оцінку кількості ітерацій для досягнення точності $\varepsilon$

\begin{equation} n \ge \left[ \log_2 \left( 1 + \frac{\ln \left( \frac{\varepsilon}{b - a} \right)}{\ln q} \right) \right] + 1. \end{equation}

Кажуть, що ітераційний метод має степінь збіжності $m$, якщо

\begin{equation} \vert x_{k + 1} - \bar x \vert = O \left( \vert x_k - \bar x \vert^m \right). \end{equation}

Для методу Ньютона

\begin{equation} \vert x_{k + 1} - \bar x \vert = \frac{\vert x_k - \bar x \vert^2 \vert \cdot f^{\prime\prime}(\xi_k) \vert}{2 \vert f’(x_k) \vert}. \end{equation}

Звідси випливає, що

\begin{equation} \vert x_{k + 1} - \bar x \vert = O\left( \vert x_k - \bar x \vert^2 \right). \end{equation}

Значить степінь збіжності методу Ньютона $m = 2$. Для методу простої ітерації і ділення навпіл $m = 1$.

Теорема 2: Нехай $f(x) \in C^2([a,b])$ та $x$ простий корінь рівняння $f(x) = 0$ ($f'(x) \ne 0$). Якщо $f'(x) \cdot f^{\prime\prime}(x) > 0$ ($f'(x) \cdot f^{\prime\prime}(x) < 0$) то для методу Ньютона при $x_0 = b$ послідовність наближень $\{x_k\}$ монотонно спадає (монотонно зростає при $x_0 = a$).

Задача 6: Довести теорему $2$ при

• $f'(x) \cdot f^{\prime\prime}(x) > 0$;

• $f'(x) \cdot f^{\prime\prime}(x) < 0$.

Задача 7: Знайти степінь збіжності методу січних [Калиткин Н.Н., Численные методы, с. 145–146]

Якщо $f(a) \cdot f^{\prime\prime}(a) > 0$ та $f^{\prime\prime}(x)$ не міняє знак, то потрібно вибирати $x_0 = a$; при цьому $\{x_k\} \uparrow \bar x$.

Якщо $f(b) \cdot f^{\prime\prime}(b) > 0$, то $x_0 = b$; маємо $\{x_k\} \downarrow \bar x$. Пояснення на рисунку 2:

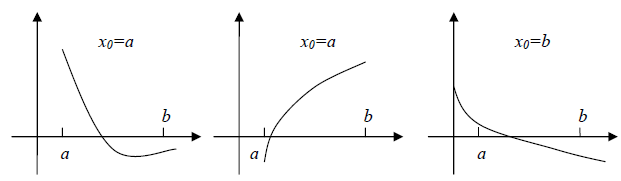
Зауваження 1: Якщо $\bar x$ — $p$-кратний корінь тобто

\begin{equation} f^{(m)}(\bar x) = 0, \quad m = 0, 1, \ldots, p - 1; \quad f^{(p)} (x) \ne 0, \end{equation}

то в методі Ньютона необхідна наступна модифікація

\begin{equation} x_{k + 1} - x_k - p \cdot \frac{f(x_k)}{f’(x_k)} \end{equation}

і

\begin{equation} q = \frac{M_{p + 1} \cdot \vert x_0 - \bar x \vert}{m_p \cdot p \cdot (p + 1)} < 1. \end{equation}

Зауваження 2: Метод Ньютона можна застосовувати і для обчислення комплексного кореня

\begin{equation} z_{k + 1} = z_k - \frac{f(z_k)}{f’(z_k)} \end{equation}

В теоремі про збіжність

\begin{equation} q = \frac{\vert x_0 - \bar x \vert M_2}{2 m_1}, \end{equation}

де

\begin{equation} m_1 = \Min_{U_r} \vert f’(z) \vert, \quad M_2 = \Max_{U_r} f^{\prime\prime}(z) \vert. \end{equation}

Тут $\vert z \vert$ — модуль комплексного числа.

Переваги методу Ньютона:

• висока швидкість збіжності;

• узагальнюється на системи рівнянь;

• узагальнюється на комплексні корені.

Недоліки методу Ньютона:

• на кожній ітерації обчислюється не тільки $f(x_k)$, а і похідна $f'(x_k)$;

• збіжність залежить від початкового наближення $x_0$, оскільки від нього залежить умова збіжності

  \begin{equation} q = \frac{M_2 \vert x_0 - \bar x \vert}{2 m_1} < 1; \end{equation}

• потрібно, щоб $f(x) \in C^2([a,b])$.