Контрольні запитання до леції №23

26. Рівняння для функцій Бесселя дійсного аргументу, функції Бесселя першого та другого роду дійсного аргументу.

При знаходженні розв’язків рівняння Пуассона та Гельмгольца в областях циліндричної форми, рівняння теплопровідності та хвильового рівняння в кругових та циліндричних областях з’являється необхідність записати розв’язки наступних звичайних диференціальних рівняння другого порядку з степеневими коефіцієнтами:

\begin{align} x^2 \cdot y’’ + x \cdot y’ + (x^2 - \nu^2) \cdot y &= 0, \label{eq:7.1} \newline x^2 \cdot y’’ + x \cdot y’ - (x^2 + \nu^2) \cdot y &= 0. \label{eq:7.2} \end{align}

У цих рівняннях $\nu$ — числовий параметр.

Визначення: Перше рівняння називають рівнянням Бесселя порядку $\nu$, а друге рівняння називають рівнянням Бесселя уявного аргументу порядку $\nu$.

Функція Бесселя першого роду

Знайти розв’язок цих рівнянь у вигляді елементарних функцій не вдається, тому враховуючи поліноміальний вигляд коефіцієнтів рівняння, можна побудувати розв’язок рівнянь у вигляді узагальненого степеневого ряду:

\begin{equation} y(x) = x^\rho \cdot (a_0 + a_1 x + a_2 x^2 + \ldots), \end{equation}

де $\rho, a_0, a_1, \ldots$ — невідомі коефіцієнти.

\begin{equation} \label{eq:7.10} J_\nu (x) = \Sum_{k = 0}^\infty \frac{(-1)^k}{\Gamma(k + \nu + 1) k!} \left( \frac{x}{2} \right)^{2 k + \nu}. \end{equation}

\begin{equation} J_{-\nu}(x) = \Sum_{k = 0}^\infty \frac{(-1)^k}{\Gamma(k - \nu + 1) k!} \left( \frac{x}{2} \right)^{2 k - \nu}. \end{equation}

Відмітимо, що визначення функції $J_{-\nu}$ є коректною лише для не цілих значень параметру $\nu$, оскільки визначення $a_0$ при $\nu = - n$ не має змісту, оскільки $\Gamma(0) = \Gamma(-1) = \ldots = \Gamma(-n) = \infty$.

Змінюючи в останній формулі індекс сумування $k = k' + n$, отримаємо

$$\begin{equation} J_{-n}(x) = (-1)^n \Sum_{k'} \frac{(-1)^{k'}}{\Gamma(k' + n + 1) \Gamma(k' + 1)} \left( \frac{x}{2} \right)^{2 k' + n} = (-1)^n J_n(x). \end{equation}$$

Остання рівність свідчить про лінійну залежність функцій $J_n(x)$ та $J_{-n}(x)$ і таким чином лінійна комбінація цих функцій не може складати загальний розв’язок рівняння Бесселя.

Функція Бесселя другого роду

Другий лінійно незалежний розв’язок рівняння Бесселя для довільного значення параметру $\nu$, взагалі кажучи не представляється у вигляді узагальненого степеневого ряду. Утворимо спеціальну лінійну комбінацію для нецілих значень параметру $\nu$:

\begin{equation} N_\nu(x) = \frac{\cos (\nu \pi) \cdot J_\nu(x) - J_{-\nu}(x)}{\sin (\nu \pi)}, \end{equation}

де $\nu \ne n$.

Остаточний вигляд функції Бесселя другого роду

$$\begin{equation} \label{eq:7.14} \begin{aligned} N_n(x) &= - \frac{1}{\pi} \Sum_{k = 0}^{n - 1} \frac{(n - k - 1)!}{k!} \left( \frac{x}{2} \right)^{2 k - n} + \frac{2}{\pi} J_n(x) \ln \frac{x}{2} - \newline & \quad - \frac{1}{\pi} \Sum_{k = 0}^\infty \frac{(-1)^k}{k! (k + n)!} \left( \frac{x}{2} \right)^{2k + n} (\Psi(k + n + 1) + \Psi(k + 1)). \end{aligned} \end{equation}$$

Дуже часто функцію Бесселя другого роду $N_\nu(x)$ називають функцією Вебера.

27. Властивості функцій Бесселя першого та другого роду дійсного аргументу.

Важливою властивістю функцій Бесселя є асимптотичний характер поведінки цих функцій на нескінченості.

Додаткові дослідження дозволяють отримати наступні асимптотичні формули:

\begin{align} J_\nu(x) &= \sqrt{\frac{2}{\pi x}} \cdot \cos \left( x - \frac{\nu \pi}{2} - \frac{\pi}{4} \right) + O \left( \frac{1}{x^{3/2}} \right), \quad x \to \infty, \newline N_{\nu}(x) &= \sqrt{\frac{2}{\pi x}} \cdot \sin \left( x - \frac{\nu \pi}{2} - \frac{\pi}{4} \right) + O \left( \frac{1}{x^{3/2}} \right), \quad x \to \infty. \end{align}

Останні формули свідчать про те, що функції Бесселя як першого так і другого роду мають злічену кількість нулів, тобто рівняння $J_\nu(x) = 0$, $N_\nu(x) = 0$ мають злічену кількість коренів, які для великих значень аргументу $x$ асимптотично прямують до нулів тригонометричних функцій $\cos \left( x - \frac{\nu \pi}{2} - \frac{\pi}{4} \right)$, $\sin \left( x - \frac{\nu \pi}{2} - \frac{\pi}{4} \right)$. А самі функції Бесселя ведуть себе як $O(1 / \sqrt{x})$, $x \to \infty$.

Аналіз формул \eqref{eq:7.10} та $(8)$ показує, що при $x \to 0$: $J_n(x) \approx \frac{1}{n!} \left( \frac{x}{2} \right)^n$, $n = 0, 1, 2, \ldots$, $N_n(x) \approx - \frac{(n - 1)!}{\pi} \left( \frac{x}{2} \right)^{-n} \to \infty$, $N_0(x) = \frac{2}{\pi} \ln \frac{x}{2} \to \infty$, $x \to 0$.

Важливою властивістю функцій Бесселя першого та другого роду є рекурентні формули, яким задовольняють функції Бесселя

\begin{align} \frac{\diff J_\nu(x)}{\diff x} + \frac{\nu}{x} \cdot J_\nu(x) &= J_{\nu - 1}(x), \newline \frac{\diff J_\nu(x)}{\diff x} - \frac{\nu}{x} \cdot J_\nu(x) &= - J_{\nu + 1}(x), \newline \frac{\diff N_\nu(x)}{\diff x} + \frac{\nu}{x} \cdot N_\nu(x) &= N_{\nu - 1}(x), \newline \frac{\diff N_\nu(x)}{\diff x} - frac{\nu}{x} \cdot N_\nu(x) &= - N_{\nu + 1}(x). \end{align}

Виключаючи з двох співвідношень похідну, можна зв’язати між собою функції Бесселя трьох сусідніх порядків.

Для прикладу наведемо графіки функцій Бесселя $J_3(x)$ та $N_3(x)$:

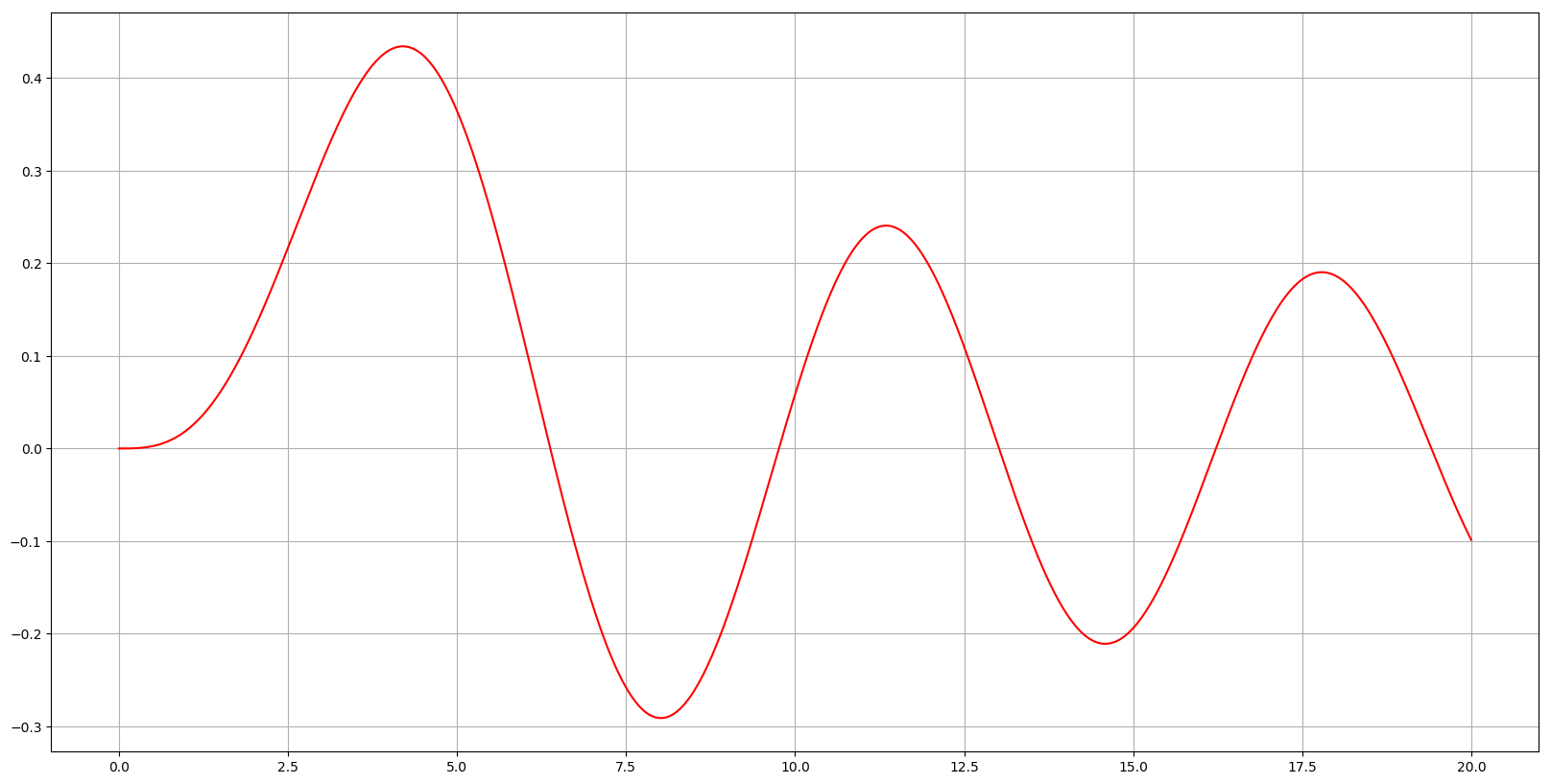
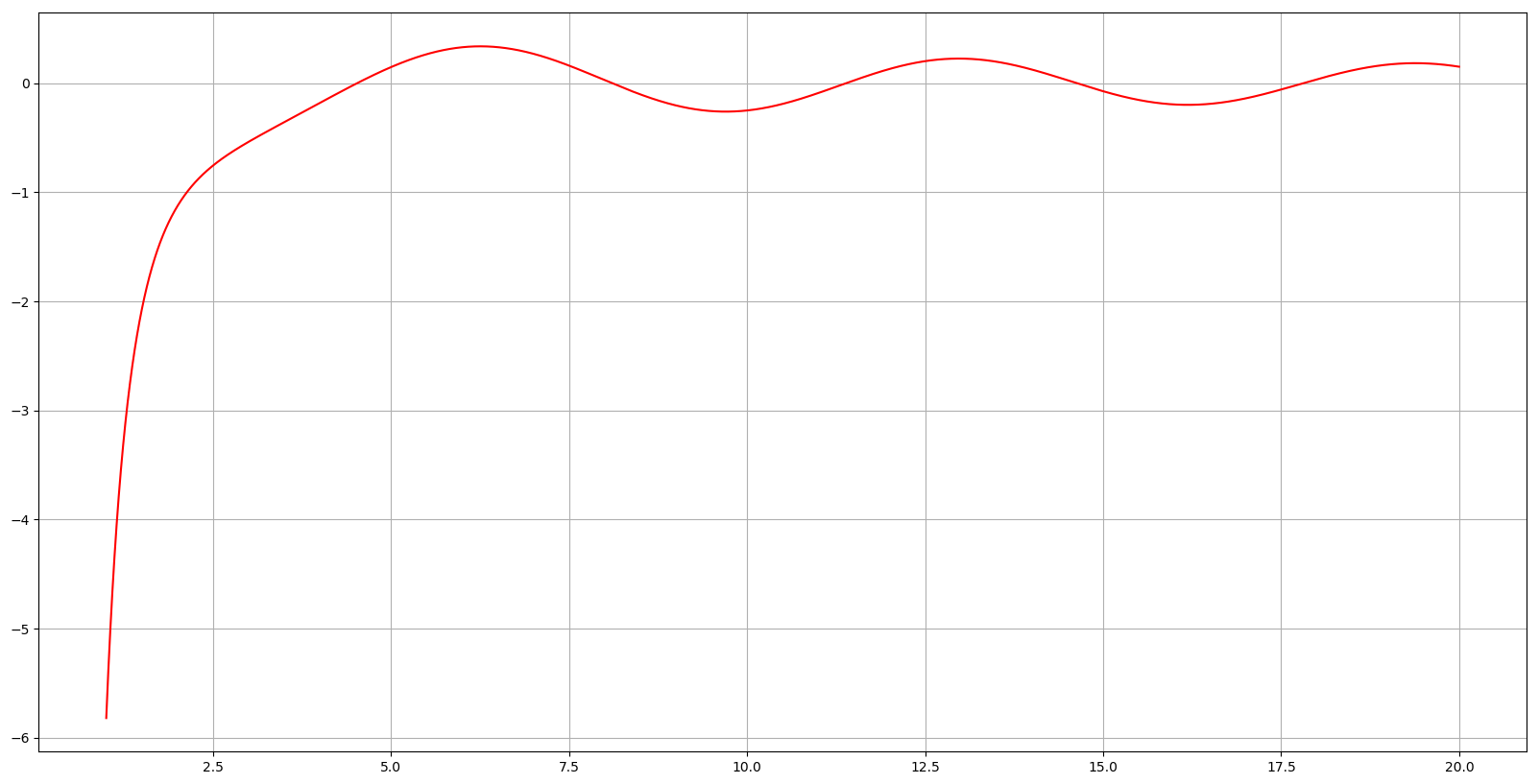
28. Рівняння для функцій Бесселя уявного аргументу, функції Бесселя першого та другого роду уявного аргументу.

При знаходженні розв’язків рівняння Пуассона та Гельмгольца в областях циліндричної форми, рівняння теплопровідності та хвильового рівняння в кругових та циліндричних областях з’являється необхідність записати розв’язки наступних звичайних диференціальних рівняння другого порядку з степеневими коефіцієнтами:

\begin{align} x^2 \cdot y’’ + x \cdot y’ + (x^2 - \nu^2) \cdot y &= 0, \newline x^2 \cdot y’’ + x \cdot y’ - (x^2 + \nu^2) \cdot y &= 0. \end{align}

У цих рівняннях $\nu$ — числовий параметр.

Визначення: Перше рівняння називають рівнянням Бесселя порядку $\nu$, а друге рівняння називають рівнянням Бесселя уявного аргументу порядку $\nu$.

Другий клас функцій Бесселя — функції Бесселя уявного аргументу можна отримати як два лінійно–незалежних розв’язки рівняння \eqref{eq:7.2}, зокрема їх можна записати за формулою \eqref{eq:7.10} з використанням заміни змінної $x \mapsto i x$, в результаті будемо мати функцію Бесселя першого роду уявного аргументу:

\begin{equation} \label{eq:7.17} I_\nu(x) = \frac{J_\nu(i x)}{i^\nu} = \Sum_{k = 0^\infty} \frac{(x / 2)^{2 k + \nu}}{k! \cdot \Gamma(k + \nu + 1)}, \quad 0 < x < \infty. \end{equation}

Другий лінійно-незалежний розв’язок для нецілих $\nu$ можна отримати аналогічно попередньому розв’язку:

\begin{equation} I_{-\nu}(x) = i^\nu J_{-\nu}(ix) = \Sum_{k = 0}^\infty \frac{(x/2)^{2k - \nu}}{k! \cdot \Gamma(k - \nu + 1)}, \quad 0 < x < \infty. \end{equation}

Легко бачити, що при $\nu = n$ функції $I_n(x) = I_{-n}(x)$ тобто є лінійно залежними між собою і не можуть бути використані для запису загального розв’язку рівняння \eqref{eq:7.2}.

Функцію другого роду уявного аргументу будують у вигляді лінійної комбінації

\begin{equation} K_\nu(x) = \frac{\pi(I_{-\nu}(x) - I_\nu(x))}{2 \sin (\nu \pi)}. \end{equation}

Функція $K_\nu(x)$ називають функцією другого роду уявного аргументу, або функцією Макдональда і вона має наступний вигляд:

$$\begin{equation} \label{eq:7.21} \begin{aligned} K_n(x) &= \frac{1}{2} \Sum_{k = 0}^{n - 1} \frac{(-1)^k \cdot (n - k - 1)!}{k!} \left( \frac{2}{x} \right)^{n - 2k} - I_n(x) \ln \frac{x}{2} + \newline & \quad + \frac{1}{2} \Sum_{k = 0}^{n - 1} \frac{(x / 2)^{n + 2 k}}{k! \cdot (k + n)!} (\Psi(k + 1) + \Psi(k + n + 1)). \end{aligned} \end{equation}$$

29. Властивості функцій Бесселя першого та другого роду уявного аргументу.

Виходячи з рекурентних співвідношень для функцій Бесселя дійсного аргументу можна отримати рекурентні співвідношення для функцій Бесселя уявного аргументу першого та другого роду:

\begin{align} \frac{\diff I_\nu(x)}{\diff x} + \frac{\nu}{x} \cdot I_\nu(x) &= I_{\nu - 1}(x), \newline \frac{\diff I_\nu(x)}{\diff x} - \frac{\nu}{x} \cdot I_\nu(x) &= - I_{\nu + 1}(x), \newline \frac{\diff K_\nu(x)}{\diff x} + \frac{\nu}{x} \cdot K_\nu(x) &= K_{\nu - 1}(x), \newline \frac{\diff K_\nu(x)}{\diff x} - frac{\nu}{x} \cdot K_\nu(x) &= - K_{\nu + 1}(x). \end{align}

Відмітимо також характер поведінки функцій Бесселя уявного аргументу при $x = 0$ та $x \to \infty$.

Виходячи з формул для \eqref{eq:7.17} та \eqref{eq:7.21} можна зробити висновок, що $I_\nu(x) = O(x^\nu)$, $x \to 0$, $K_\nu(x) = O(x^{-\nu})$, $\nu > 0$, $K_0(x) = O(\ln(x))$, $x \to 0$, $I_\nu(x) \approx \sqrt{\frac{1}{2 \pi x}} \cdot e^x$, $K_\nu(x) \approx \sqrt{\frac{\pi}{2 x}} \cdot e^{-x}$, $x \to \infty$.

Наведемо графіки функцій $I_3(x)$ та $K_3(x)$:

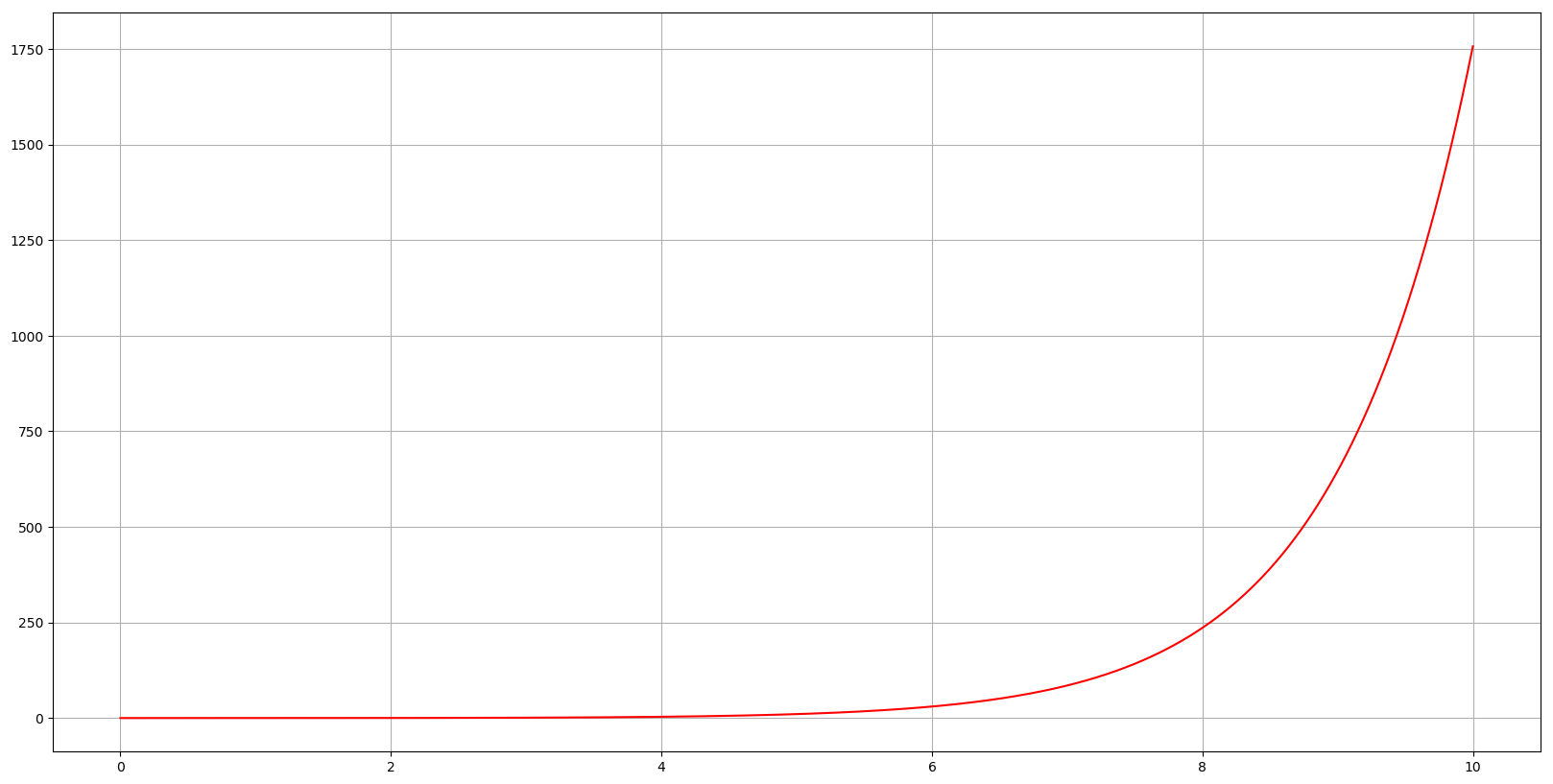
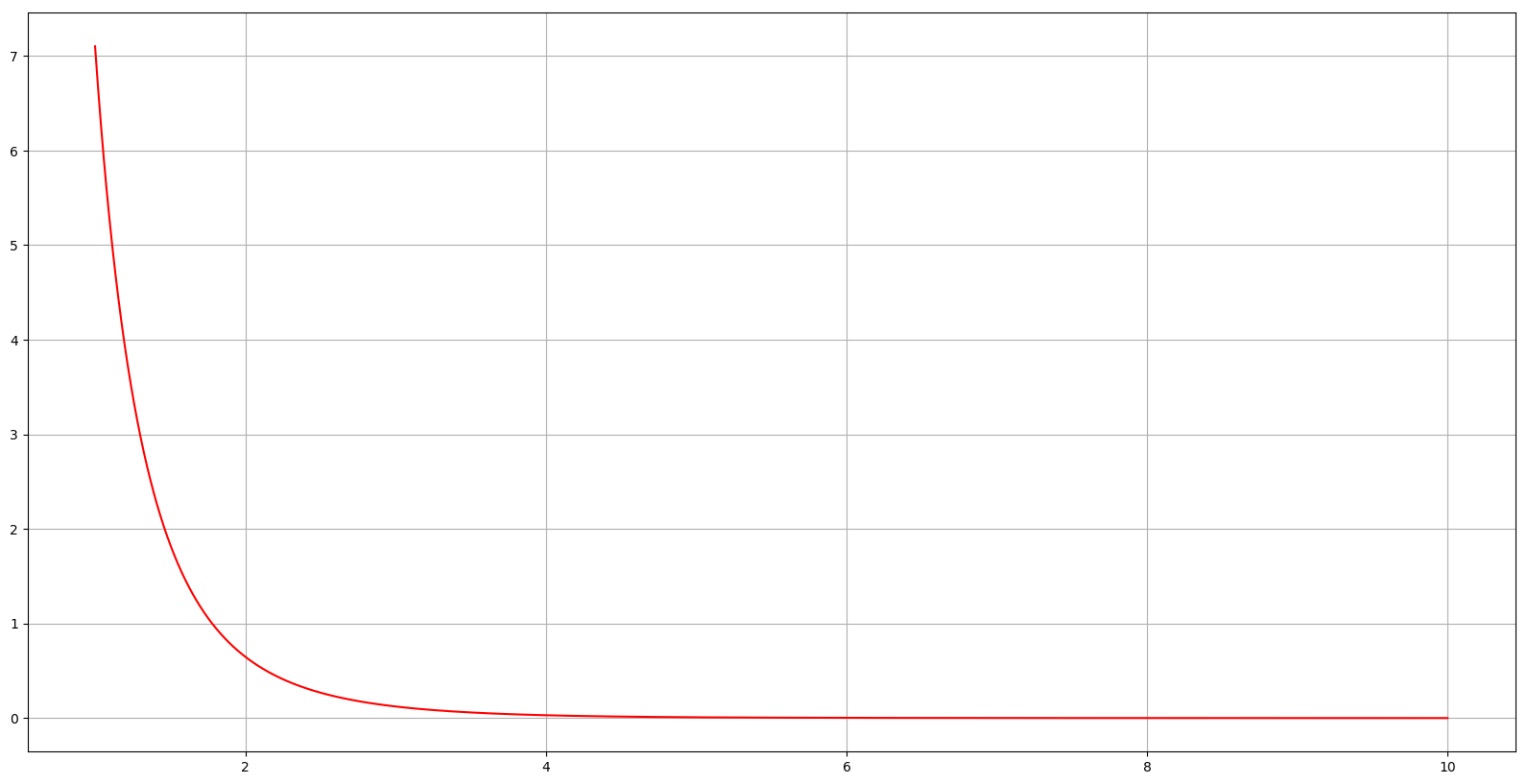
36. Приклади неєдиності розв’язку зовнішньої граничних задач рівняння Гельмгольца, природа неєдиності, умови Зомерфельда.

Розглянемо приклад зовнішньої задачі для однорідного рівняння Гельмгольца:

$$\begin{equation} \left\{ \begin{aligned} & \Delta u(x) + k^2 u = 0, \quad |x| > \pi, \newline & \left. u(x) \right\vert_{|x| = \pi} = 0, \newline & u(x) \xrightarrow[|x| \to \infty]{} 0, \end{aligned} \right. \end{equation}$$

де $x = \begin{pmatrix} x_1 & x_2 & x_3 \end{pmatrix}$.

При $k = 0$ гранична задача має лише тривіальний розв’язок тотожньо рівний нулю, що випливає з другої теореми єдиності гармонічних функцій. У випадку, коли $k$ — ціле ми маємо, що розв’язком останньої граничної задачі окрім тотожного нуля буде функція $u(x) = \frac{\sin (x \vert x \vert)}{4 \pi \vert x \vert}$. Легко перевірити, що ця функція задовольняє як однорідному рівнянню Гельмгольца (це уявна частина фундаментального розв’язку) так і граничній умові на сфері і умові на нескінченості.

Наявність нетривіального розв’язку у однорідної задачі означає неєдиність розв’язку відповідної неоднорідної задачі.

Для виділення єдиного розв’язку зовнішньої задачі задаються умови поведінки розв’язку задачі в нескінченно віддаленій точці. Ці умови називають умовами випромінювання або умовами Зомерфельда:

\begin{align} & u(x) = O (|x|^{-1}), \quad \frac{\partial u(x)}{\partial |x|} - i k u(x) = o(|x|^{-1}), \quad |x| \to \infty, \newline & u(x) = O (|x|^{-1}), \quad \frac{\partial u(x)}{\partial |x|} + i k u(x) = o(|x|^{-1}), \quad |x| \to \infty. \end{align}

Перша умова відповідає хвилям, що уходять на нескінченість, друга — хвилям, що приходять з нескінченості.

Саме ці умови забезпечують єдність розв’язку зовнішніх граничних задач для рівняння Гельмгольца.

У випадку рівняння Гельмгольца на площині умови Зомерфельда мають вигляд:

\begin{align} & u(x) = O (|x|^{-1/2}), \quad \frac{\partial u(x)}{\partial |x|} - i k u(x) = o(|x|^{-1/2}), \quad |x| \to \infty, \newline & u(x) = O (|x|^{-1/2}), \quad \frac{\partial u(x)}{\partial |x|} + i k u(x) = o(|x|^{-1/2}), \quad |x| \to \infty. \end{align}